题目内容
如图1所示为某仪器内部结构图,由O1处静止释放的电子经加速电压U1加速后沿横截面为正方形的金属盒中轴线O2O3射入金属盒,O2为金属盒左端面的中心,金属盒由上下两个水平放置、前后两个竖直放置,长为L1、宽为L0的金属薄板组成(它们不相连),金属盒横截面如图2,距盒右端面L2处有一面积足够大并与O2O3相垂直的接收屏,屏中心为O,O1O2O3O在同一水平直线上.屏上所设直角坐标轴的X轴垂直纸面向外.仪器可在盒前、后两面及上、下两面加如图3所示的UXX′-t扫描电压及UYY′-t的正弦交流电压.设电子的质量为m,带电量为e,图中U0、T均为已知量.设所有入射的电子均能到达屏,不计电子所受重力、电子间的相互作用及电子由静止释放到O2的运动时间.在每个电子通过电场的极短时间内,电场可视作恒定的.
(1)如仪器只提供UXX′-t扫描电压,请定性说明t=T/4时刻入射的电子在盒内及离盒后各做什么运动;
(2)如仪器只提供UXX′-t扫描电压,试计算t=T/4时刻入射的电子打在屏上的坐标;
(3)如果在盒内同时具有UXX′-t扫描电压和UYY′-t的正弦交流电压,请在答题卡上提供的坐标图上标出t=T/2至t=3T/2时间段入射的电子打在屏上所留下的痕迹示意图,其中坐标图上每单位长度为
[不要求计算过程].

(1)如仪器只提供UXX′-t扫描电压,请定性说明t=T/4时刻入射的电子在盒内及离盒后各做什么运动;
(2)如仪器只提供UXX′-t扫描电压,试计算t=T/4时刻入射的电子打在屏上的坐标;
(3)如果在盒内同时具有UXX′-t扫描电压和UYY′-t的正弦交流电压,请在答题卡上提供的坐标图上标出t=T/2至t=3T/2时间段入射的电子打在屏上所留下的痕迹示意图,其中坐标图上每单位长度为
| L1(L1+2L2)U0 | 8L0U1 |
分析:(1)提供UXX′-t扫描电压,电场在XX′方向,电子进入磁场受电场力,电场力与速度方向垂直,做类平抛运动,出电场后,电子不受力,电子做匀速直线运动.
(2)求出
时刻入射时,在XX′方向上的电势差,从而求出电场强度,根据牛顿第二定律求出该方向上的加速度,从而求出离开电场时的偏转位移,出电场后做匀速直线运动,将该运动分解为x轴方向和OO1方向,根据OO1方向求出运动的时间,从而求出x轴方向上的位移,两个位移之和即为打在屏上的横坐标.
(3)分析出在
~
内在x轴方向和y轴方向偏移量与所加电压的关系,从而作出入射的电子打在屏上所留下的痕迹示意图.
(2)求出
| T |
| 4 |
(3)分析出在
| T |
| 2 |
| 3T |
| 2 |
解答:解:(1)在盒内做类平抛运动,离盒后做匀速直线运动.
(2)设离盒时x方向的侧移为x1,在盒内运动的时间为t1,离盒后到屏的运动时间为t2,最终打在屏上x坐标为x.
eU1=
mv02
x1=
at12 a=
E=
t1=
t2=
x=x1+△x,又△x=a1t1t2.
联立各式解得:x=
.
所以打在屏上的坐标为(
,0)
(3)痕迹如图所示.
 答:(1)在盒内做类平抛运动,离盒后做匀速直线运动.
答:(1)在盒内做类平抛运动,离盒后做匀速直线运动.
(2)打在屏上的坐标为(
,0)
(3)痕迹如图所示.
(2)设离盒时x方向的侧移为x1,在盒内运动的时间为t1,离盒后到屏的运动时间为t2,最终打在屏上x坐标为x.
eU1=
| 1 |
| 2 |
x1=
| 1 |
| 2 |
| eE |
| m |
E=
| ||
| L0 |
t1=
| L1 |
| v0 |
| L2 |
| v0 |
x=x1+△x,又△x=a1t1t2.
联立各式解得:x=
| L1(L1+2L2)U0 |
| 8L0U1 |
所以打在屏上的坐标为(
| L1(L1+2L2)U0 |
| 8L0U1 |
(3)痕迹如图所示.
 答:(1)在盒内做类平抛运动,离盒后做匀速直线运动.
答:(1)在盒内做类平抛运动,离盒后做匀速直线运动.(2)打在屏上的坐标为(
| L1(L1+2L2)U0 |
| 8L0U1 |
(3)痕迹如图所示.
点评:解决本题的关键理清电子的运动过程,将电子的运动过程分解成x方向和y方向,通过电子的运动情况,结合牛顿定律和运动学公式求出偏移量.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目


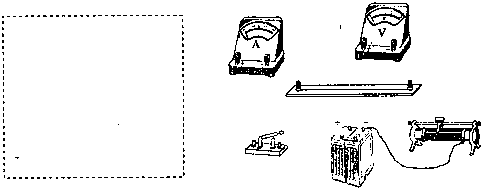

 表示),要测量它的伏安特性,另提供有下列的实验器材:电源E(电动势为4V,内阻不计);滑线变阻器R0(阻值0-20Ω);毫安表
表示),要测量它的伏安特性,另提供有下列的实验器材:电源E(电动势为4V,内阻不计);滑线变阻器R0(阻值0-20Ω);毫安表 (量程20mA,有内阻);数字万用表(电压挡
(量程20mA,有内阻);数字万用表(电压挡 有五个量程:分别为0.2V、2V、20V、200V,2000V,内阻很大);开关一只;导线若干.
有五个量程:分别为0.2V、2V、20V、200V,2000V,内阻很大);开关一只;导线若干.

 [不要求计算过程].
[不要求计算过程].