题目内容
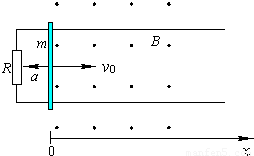 如图所示,两条互相平行的光滑金属导轨位于水平面内,距离为l=0.2m,在导轨的一端接有阻值为R=0.5Ω的电阻,在x≥0处有与水平面垂直的均匀磁场,磁感应强度B=0.5T.一质量为m=0.1kg的金属直杆垂直放置在导轨上,并以v=2m/s的初速度进入磁场,在安培力和一垂直于杆的水平外力F的共同作用下做匀变速直线运动,加速度大小为a=2m/s2,方向与初速度方向相反.设导轨和金属杆的电阻都可以忽略,且接触良好,求:
如图所示,两条互相平行的光滑金属导轨位于水平面内,距离为l=0.2m,在导轨的一端接有阻值为R=0.5Ω的电阻,在x≥0处有与水平面垂直的均匀磁场,磁感应强度B=0.5T.一质量为m=0.1kg的金属直杆垂直放置在导轨上,并以v=2m/s的初速度进入磁场,在安培力和一垂直于杆的水平外力F的共同作用下做匀变速直线运动,加速度大小为a=2m/s2,方向与初速度方向相反.设导轨和金属杆的电阻都可以忽略,且接触良好,求:(1)电流为零时金属杆所处的位置;
(2)电流为最大值的一半时施加在金属杆上外力F的大小和方向.
【答案】分析:(1)电流为0时,电动势为0,切割的速度为0.即知电流为0的位置为金属杆匀减速运动速度为0的位置,根据匀变速运动的公式求出金属杆的位移.
(2)当速度为v时,电动势最大,电流最大,根据E=BLv,结合闭合电路欧姆定律,可以求出最大电流.从而可以求出电流为最大值的一半时所受的安培力,根据牛顿第二定律求出外力的大小和方向.(要考虑金属杆的运动方向)
解答:解:(1)感应电动势E=Blv,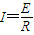 ,故I=0时v=0,
,故I=0时v=0,
则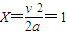 m.
m.
(2)最大电流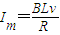 ,
,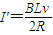 .
.
安培力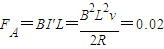 N,
N,
向右运动时,F+FA=ma,F=ma-FA=0.18,方向与x轴相反
向左运动时,F-FA=ma,F=ma+FA=0.22N,方向与x轴相反
答:(1)电流为零时金属杆所处的位置X=1m;
(2)电流为最大值的一半时施加在金属杆上外力F的大小和方向:
向右运动时,F+FA=ma,F=ma-FA=0.18,方向与x轴相反
向左运动时,F-FA=ma,F=ma+FA=0.22N,方向与x轴相反.
点评:解决本题的关键正确地对金属杆进行受力分析,灵活运用牛顿第二定律.以及掌握导体棒切割磁感线产生的感应电动势E=BLv.
(2)当速度为v时,电动势最大,电流最大,根据E=BLv,结合闭合电路欧姆定律,可以求出最大电流.从而可以求出电流为最大值的一半时所受的安培力,根据牛顿第二定律求出外力的大小和方向.(要考虑金属杆的运动方向)
解答:解:(1)感应电动势E=Blv,
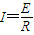 ,故I=0时v=0,
,故I=0时v=0,则
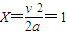 m.
m.(2)最大电流
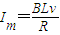 ,
,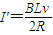 .
.安培力
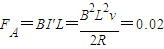 N,
N,向右运动时,F+FA=ma,F=ma-FA=0.18,方向与x轴相反
向左运动时,F-FA=ma,F=ma+FA=0.22N,方向与x轴相反
答:(1)电流为零时金属杆所处的位置X=1m;
(2)电流为最大值的一半时施加在金属杆上外力F的大小和方向:
向右运动时,F+FA=ma,F=ma-FA=0.18,方向与x轴相反
向左运动时,F-FA=ma,F=ma+FA=0.22N,方向与x轴相反.
点评:解决本题的关键正确地对金属杆进行受力分析,灵活运用牛顿第二定律.以及掌握导体棒切割磁感线产生的感应电动势E=BLv.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
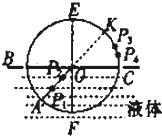 学校开展研究性学习,某研究小组的同学根据所学的光学知识,设计了一个测量液体折射率的仪器,如图所示.在一圆盘上,过其圆心O作两条互相垂直的直径BC、EF,在半径OA上,垂直盘面插下两枚大头针P1、P2并保持P1、P2位置不变,每次测量时让圆盘的下半部分竖直进入液体中,而且总使得液面与直径BC相平,EF作为界面的法线,而后在图中右上方区域观察P1、P2的像,并在圆周上插上大头针P3,使P3正好挡住P1、P2的像.同学们通过计算,预先在圆周EC部分刻好了折射率的值,这样只要根据P3所插的位置,就可直接读出液体折射率的值,若∠AOF=30°则( )
学校开展研究性学习,某研究小组的同学根据所学的光学知识,设计了一个测量液体折射率的仪器,如图所示.在一圆盘上,过其圆心O作两条互相垂直的直径BC、EF,在半径OA上,垂直盘面插下两枚大头针P1、P2并保持P1、P2位置不变,每次测量时让圆盘的下半部分竖直进入液体中,而且总使得液面与直径BC相平,EF作为界面的法线,而后在图中右上方区域观察P1、P2的像,并在圆周上插上大头针P3,使P3正好挡住P1、P2的像.同学们通过计算,预先在圆周EC部分刻好了折射率的值,这样只要根据P3所插的位置,就可直接读出液体折射率的值,若∠AOF=30°则( )| A、用该装置能测量所有液体的折射率 | ||
| B、图中P3位置处所对应的折射率P4处的大 | ||
| C、作AO的延长线交圆周于K,K处所对应的折射率值应为1 | ||
D、若OP3与OC的夹角为30°,则P3处所对应的折射率的值为
| ||
| E、测某液体折射率时,在右上方区域观察不到P1、P2的像,说明该液体的折射率大于2 |
 (2007?南开区模拟)学校开展研究性学习.某研究小组的同学根据所学的光学知识,设计了一个测液体折射率的仪器.如图所示,在一个圆盘上过其圆心0作两条互相垂直的直径BC、EF,在半径OA上垂直盘面插下两枚大头针P1、P2并保持P1、P1位置不变,每次测量时让圆盘的下半部分竖直进入液体中,而且总使得液面与直径BC相平,EF作为界面的法线,而后在图中右上方区域观察Pl、P2的像,并在圆周上插上大头针P3,使P3正好挡住Pl、P2,同学们通过计算,预先在圆周EC部分刻好了折射率的值.这样只要根据P3所插的位置,就可直接读出液体折射率的值.则:
(2007?南开区模拟)学校开展研究性学习.某研究小组的同学根据所学的光学知识,设计了一个测液体折射率的仪器.如图所示,在一个圆盘上过其圆心0作两条互相垂直的直径BC、EF,在半径OA上垂直盘面插下两枚大头针P1、P2并保持P1、P1位置不变,每次测量时让圆盘的下半部分竖直进入液体中,而且总使得液面与直径BC相平,EF作为界面的法线,而后在图中右上方区域观察Pl、P2的像,并在圆周上插上大头针P3,使P3正好挡住Pl、P2,同学们通过计算,预先在圆周EC部分刻好了折射率的值.这样只要根据P3所插的位置,就可直接读出液体折射率的值.则: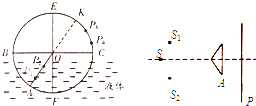 Ⅰ学校开展研究性学习,某研究小组的同学根据所学的光学知识,设计了一个测量液体折射率的仪器,如图所示.在一圆盘上,过其圆心O作两条互相垂直的直径BC、EF,在半径OA上,垂直盘面插下两枚大头针P1、P2,并保持P1、P2位置不变,∠AOF=30°,每次测量时让圆盘的下半部分竖直进入液体中,而且总使得液面与直径BC相平,EF作为界面的法线,而后在图中右上方区域观察P1、P2的像,并在圆周上插上大头针P3,使P3正好挡住P1、P2的像,同学们通过计算,预先在圆周EC部分刻好了折射率的值,这样只要根据P3所插的位置,就可直接读出液体折射率的值,则:
Ⅰ学校开展研究性学习,某研究小组的同学根据所学的光学知识,设计了一个测量液体折射率的仪器,如图所示.在一圆盘上,过其圆心O作两条互相垂直的直径BC、EF,在半径OA上,垂直盘面插下两枚大头针P1、P2,并保持P1、P2位置不变,∠AOF=30°,每次测量时让圆盘的下半部分竖直进入液体中,而且总使得液面与直径BC相平,EF作为界面的法线,而后在图中右上方区域观察P1、P2的像,并在圆周上插上大头针P3,使P3正好挡住P1、P2的像,同学们通过计算,预先在圆周EC部分刻好了折射率的值,这样只要根据P3所插的位置,就可直接读出液体折射率的值,则: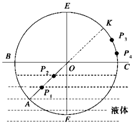 学校开展研究性学习,某研究小组的同学根据所学的光学知识,设计了一个测量液体折射率的仪器,如图所示.在一圆盘上,过其圆心O作两条互相垂直的直径BC、EF,在半径OA上,垂直盘面插下两枚大头针P1、P2并保持P1、P2位置不变,每次测量时让圆盘的下半部分竖直进入液体中,而且总使得液面与直径BC相平,EF作为界面的法线,而后在图中右上方区域观察P1、P2的像,并在圆周上插上大头针P3,使P3正好挡住P1、P2的像,同学们通过计算,预先在圆周EC部分刻好了折射率的值,这样只要根据P3所插的位置,就可直接读出液体折射率的值,则:
学校开展研究性学习,某研究小组的同学根据所学的光学知识,设计了一个测量液体折射率的仪器,如图所示.在一圆盘上,过其圆心O作两条互相垂直的直径BC、EF,在半径OA上,垂直盘面插下两枚大头针P1、P2并保持P1、P2位置不变,每次测量时让圆盘的下半部分竖直进入液体中,而且总使得液面与直径BC相平,EF作为界面的法线,而后在图中右上方区域观察P1、P2的像,并在圆周上插上大头针P3,使P3正好挡住P1、P2的像,同学们通过计算,预先在圆周EC部分刻好了折射率的值,这样只要根据P3所插的位置,就可直接读出液体折射率的值,则: