题目内容
如图所示,为t1、t2两时刻的波形图,t1=0,t2=0.5s,3T<t2-t1<4T.若波由左向右传,波速为 m/s;若v=74m/s,波应向X轴 (填:正或负)方向传播.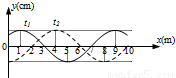
【答案】分析:若波由左向右传,根据波形的平移法可知,波传播的距离最短距离为3m,由题3T<t2-t1<4T,结合波在一个周期内传播的距离是一个波长,即可得到在t2-t1时间内波传播的距离△x,由v=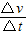 求出波速.
求出波速.
若v=74m/s,波传播的距离为△x=vt,根据△x与波长的关系,判断波的传播方向.
解答:解:(1)由图读出波长λ=8m,若波由左向右传,3T<t2-t1<4T,则在t2-t1时间内波传播的距离△x=3λ+3m=27m,
则波速v=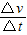 =
= =54m/s
=54m/s
(3)若v=74m/s,波传播的距离为△x=vt=74×0.5m=37m=4λ+5m,结合图形,知波向x轴负方向传播.
故答案为:54,负.
点评:本题要抓住波周期性,运用波形的平移法得到波的传播距离,并根据波传播距离判断波的传播方向.
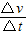 求出波速.
求出波速.若v=74m/s,波传播的距离为△x=vt,根据△x与波长的关系,判断波的传播方向.
解答:解:(1)由图读出波长λ=8m,若波由左向右传,3T<t2-t1<4T,则在t2-t1时间内波传播的距离△x=3λ+3m=27m,
则波速v=
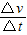 =
= =54m/s
=54m/s(3)若v=74m/s,波传播的距离为△x=vt=74×0.5m=37m=4λ+5m,结合图形,知波向x轴负方向传播.
故答案为:54,负.
点评:本题要抓住波周期性,运用波形的平移法得到波的传播距离,并根据波传播距离判断波的传播方向.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 “在某次蹦极中,弹性绳弹力F的大小随时间t的变化图象如图所示,其中t1、t3时刻图线的斜率最大.将蹦极过程近似为在竖直方向的运动,弹性绳中弹力与伸长量的关系遵循胡克定律,空气阻力不计.下列说法正确的是( )
“在某次蹦极中,弹性绳弹力F的大小随时间t的变化图象如图所示,其中t1、t3时刻图线的斜率最大.将蹦极过程近似为在竖直方向的运动,弹性绳中弹力与伸长量的关系遵循胡克定律,空气阻力不计.下列说法正确的是( )| A、t1~t2时间内运动员处于超重状态 | B、t2~t4时间内运动员的机械能先增大后减小 | C、t3时刻运动员的加速度为零 | D、t4时刻运动员具有向上的最大速度 |
 物体某段过程的v-t图象如图所示,在t1和t2时刻的瞬时速度分别为V1和V2,则在t1~t2过程中( )
物体某段过程的v-t图象如图所示,在t1和t2时刻的瞬时速度分别为V1和V2,则在t1~t2过程中( ) 如图所示,为测定导轨上滑块的加速度,滑块上安装了宽度为2.8cm的遮光板.滑块在牵引力作用下先后通过两个光电门,配套的数字毫秒计(图中未画出)记录了遮光板通过第一个光电门的时间为△t1=0.28s,则滑块通过第一个光电门的速度为
如图所示,为测定导轨上滑块的加速度,滑块上安装了宽度为2.8cm的遮光板.滑块在牵引力作用下先后通过两个光电门,配套的数字毫秒计(图中未画出)记录了遮光板通过第一个光电门的时间为△t1=0.28s,则滑块通过第一个光电门的速度为
 如图所示,为甲、乙两物体做直线运动的s-t图象,则下列说法中不正确的是( )
如图所示,为甲、乙两物体做直线运动的s-t图象,则下列说法中不正确的是( )