题目内容
如图所示，足够长的矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场，现从ad边的中心O点处，垂直磁场方向射入一速度为v0的带正电粒子，v0与ad边的夹角为30°．已知粒子质量为m，带电量为q，ad边长为L，不计粒子的重力．（1）求要使粒子能从ab边射出磁场，v0的大小范围．
（2）粒子在磁场中运动的最长时间是多少？在这种情况下，粒子将从什么范围射出磁场？
分析：（1）根据牛顿第二定律，由洛伦兹力提供向心力，结合几何关系可确定半径的范围，即可求解；
（2）根据题意确定运动轨迹，再由圆心角与周期公式，即可确定最长运动的时间；根据半径公式与半径的取值，即可求解．
（2）根据题意确定运动轨迹，再由圆心角与周期公式，即可确定最长运动的时间；根据半径公式与半径的取值，即可求解．
解答：解：（1）粒子带正电，粒子运动的轨迹如图所示，当粒子的速度大于与R1相对应的速度v1时，粒子将恰好不从dc边射出．
由几何关系可得：R1=L ①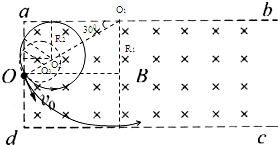
由洛仑兹力和向心力公式可得：qv1B=m
②
当粒子的速度小于与R2相对应的速度v2时，粒子将从ad边射出．
由几何关系可得：R2+R2sin30°=
L ③
由③式解得：R2=
L ④
由洛仑兹力和向心力公式可得：qv2B=m
⑤
将①④式分别代入②⑤式可解得：v1=
；v2=
⑥
所以v0的取值范围是
＜v0≤
⑦
（2）若粒子在磁场中运动的时间最长，其对应的圆周运动的圆心角必然最大，在答图中，当粒子的速度小于v2时，粒子从ad边的不同位置射出时，其半径虽不同，但圆心角的夹角都是
×2π，所以粒子在磁场中的运动时间也是
，此即粒子在磁场中运动的最长时间．
粒子运动的周期：T=
=
所以粒子运动的最长时间为：t=
T=
⑧
粒子恰好没从ab边射出时，设粒子的轨迹与ad边交与P点，则：
=2?R2sin30°=R2=
L
即：粒子将从O点上方的
L的范围内射出磁场．
答：（1）使粒子能从ab边射出磁场，v0的取值范围
＜v0≤
，
（2）粒子在磁场中运动的最长时间是t=
；在这种情况下，粒子将从O点上方的
L的范围内射出磁场．
由几何关系可得：R1=L ①
由洛仑兹力和向心力公式可得：qv1B=m
| ||
| R1 |
当粒子的速度小于与R2相对应的速度v2时，粒子将从ad边射出．
由几何关系可得：R2+R2sin30°=
| 1 |
| 2 |
由③式解得：R2=
| 1 |
| 3 |
由洛仑兹力和向心力公式可得：qv2B=m
| ||
| R2 |
将①④式分别代入②⑤式可解得：v1=
| qBL |
| m |
| qBL |
| 3m |
所以v0的取值范围是
| qBL |
| 3m |
| qBL |
| m |
（2）若粒子在磁场中运动的时间最长，其对应的圆周运动的圆心角必然最大，在答图中，当粒子的速度小于v2时，粒子从ad边的不同位置射出时，其半径虽不同，但圆心角的夹角都是
| 5 |
| 6 |
| 5T |
| 6 |
粒子运动的周期：T=
| 2πR |
| v |
| 2πm |
| qB |
所以粒子运动的最长时间为：t=
| 5 |
| 6 |
| 5πm |
| 3qB |
粒子恰好没从ab边射出时，设粒子的轨迹与ad边交与P点，则：
. |
| OP |
| 1 |
| 3 |
即：粒子将从O点上方的
| 1 |
| 3 |
答：（1）使粒子能从ab边射出磁场，v0的取值范围
| qBL |
| 3m |
| qBL |
| m |
（2）粒子在磁场中运动的最长时间是t=
| 5πm |
| 3qB |
| 1 |
| 3 |
点评：考查牛顿第二定律的应用，掌握几何关系在题中的运用，理解在磁场中运动时间与圆心角的关系．注意本题关键是画出正确的运动轨迹．
练习册系列答案
综合自测系列答案
相关题目
