Question

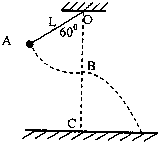如图所示，初态细线OA与竖直方向OB夹角为60°，让摆球从图中A位置由静止开始下摆，正好到最低点B位置时线被拉断，设摆线长L=1.6m，悬点O与地面的竖直高度OC=6.6m，不计空气阻力，求摆球着地时距c多远？（g取10m/s²）

Answer 1

分析：摆球由A位置摆到最低点B位置的过程中，只有重力对摆球做功，其机械能守恒．由机械能守恒定律求出摆球摆到最低点B位置时的速度，线被拉断后做平抛运动，根据平抛运动的基本公式求出水平距离．

解答：解：摆球由A位置摆到最低点B位置的过程中，由机械能守恒得：
mg（L-L cos60°）=

1

2

mvB2
代人数据解得：v_B=

2gL(1-cos60°)

=

2×10×1.6×0.5

=4m/s
线被拉断后做平抛运动，则有：
t=

2(H-L) g

=

2(6.6-1.6) 10

=1s
所以C、D间距：x=v_Bt=4×1m=4m   
答：摆球着地时距c点4m远．

点评：本题是圆周运动与平抛运动的综合，采用程序法分析求解．两个过程机械能都守恒．属于基础题．