题目内容
一块足够长的白板,位于水平桌面上,处于静止状态.一石墨块(可视为质点)静止在白板上.石墨块与白板间有摩擦,滑动摩擦系数为μ.突然,使白板以恒定的速度v做匀速直线运动,石墨块将在板上划下黑色痕迹.经过某段时间t,令白板突然停下,以后不再运动.在最后石墨块也不再运动时,白板上黑色痕迹的长度可能是(已知重力加速度为g,不计石墨与板摩擦划痕过程中损失的质量):①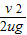 ②
②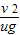 ③
③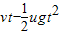 ④vt,以上正确的是( )
④vt,以上正确的是( )A.①③
B.①④
C.②③
D.②④
【答案】分析:石墨在白板上受到重力、支持力和摩擦力,根据牛顿第二定律求解出加速度,根据运动学公式求出相对滑动的位移即可.
解答:解:在时间t内,石墨可能一直匀加速,也可能先加速后匀速;
石墨加速时,根据牛顿第二定律,有
μmg=ma
解得
a=μg
①如果时间t内一直加速,加速的位移为x1= μgt2,故相对白板的位移为△x1=vt-x1=vt-
μgt2,故相对白板的位移为△x1=vt-x1=vt- μgt2
μgt2
②如果先加速,后匀速,位移为x2=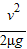 +v(t-
+v(t-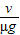 )=vt-
)=vt-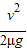 ,故相对白板的位移为△x2=vt-x2=
,故相对白板的位移为△x2=vt-x2=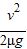
③如果加速的末速度恰好等于v,则x3=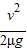 ,故相对白板的位移为△x3=vt-x3=
,故相对白板的位移为△x3=vt-x3=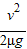
经过时间t后,白板静止后,石墨做减速运动,加速度大小不变,故相对白板沿原路返回,故白板上黑色痕迹的长度等于加速时相对薄板的位移;
所以白板上黑色痕迹的长度可能是:①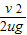 、③
、③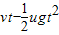
故选A.
点评:本题也可以薄板为参考系,则石墨先加速前进,后减速沿原来返回,提供运动学公式列式分析即可.
解答:解:在时间t内,石墨可能一直匀加速,也可能先加速后匀速;
石墨加速时,根据牛顿第二定律,有
μmg=ma
解得
a=μg
①如果时间t内一直加速,加速的位移为x1=
 μgt2,故相对白板的位移为△x1=vt-x1=vt-
μgt2,故相对白板的位移为△x1=vt-x1=vt- μgt2
μgt2②如果先加速,后匀速,位移为x2=
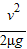 +v(t-
+v(t-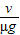 )=vt-
)=vt-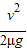 ,故相对白板的位移为△x2=vt-x2=
,故相对白板的位移为△x2=vt-x2=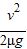
③如果加速的末速度恰好等于v,则x3=
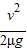 ,故相对白板的位移为△x3=vt-x3=
,故相对白板的位移为△x3=vt-x3=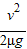
经过时间t后,白板静止后,石墨做减速运动,加速度大小不变,故相对白板沿原路返回,故白板上黑色痕迹的长度等于加速时相对薄板的位移;
所以白板上黑色痕迹的长度可能是:①
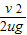 、③
、③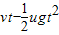
故选A.
点评:本题也可以薄板为参考系,则石墨先加速前进,后减速沿原来返回,提供运动学公式列式分析即可.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
 突然,使白板以恒定的速度
突然,使白板以恒定的速度 做匀速直线运动,石墨块将在板上划下黑色痕迹.经过某一时间
做匀速直线运动,石墨块将在板上划下黑色痕迹.经过某一时间 ,令白板突然停下,以后不再运动.在最后石墨块也不再运动时,白板上黑色痕迹的长度可能是(已知重力加速度为g,不计石墨与板摩擦划痕过程中损失的质量)( )
,令白板突然停下,以后不再运动.在最后石墨块也不再运动时,白板上黑色痕迹的长度可能是(已知重力加速度为g,不计石墨与板摩擦划痕过程中损失的质量)( ) B.
B. C.
C. D.
D.
 做匀速直线运动,石墨块将在板上划下黑色痕迹。经过某段时间t,令白板突然停下,以后不再运动。在最后石墨块也不再运动时,白板上黑色痕迹的长度可能是(已知重力加速度为g,不计石墨与板摩擦划痕过程中损失的质量):1
做匀速直线运动,石墨块将在板上划下黑色痕迹。经过某段时间t,令白板突然停下,以后不再运动。在最后石墨块也不再运动时,白板上黑色痕迹的长度可能是(已知重力加速度为g,不计石墨与板摩擦划痕过程中损失的质量):1 、 2
、 2 、
、 μgt2、 4 v0 t ,以上正确的是
μgt2、 4 v0 t ,以上正确的是