题目内容
如图所示，木块A、B分别重50N和60N，它们与水平地面间的动摩擦因数均为0.25，夹在A、B之间的轻弹簧被压缩了2cm，弹簧的劲度系数为400N/m，系统置于水平地面上静止不动．现用F=1N的水平拉力作用在木块B上，力F作用后（ ）分析：先求解出木块A、B的最大静摩擦力，然后求解出弹簧弹力，最后对两个木块分别受力分析后分析求解．
解答：解：弹簧弹力为：F1=kx=400N/m×0.02m=8N；
A木块与地面间的最大静摩擦力为：fAm=μGA=0.25×50N=12.5N；
B木块与地面间的最大静摩擦力为：fBm=μGB=0.25×60N=15N；
用F=1N的水平拉力作用在木块B上，木块B受弹簧向右的弹力为8N．拉力为1N，共9N，小于最大静摩擦力，故静摩擦力为9N，向左；
A、B、木块A受到向左的弹力为8N，小于最大静摩擦力，故A不动，故静摩擦力为8N，向右；
故选AD
A木块与地面间的最大静摩擦力为：fAm=μGA=0.25×50N=12.5N；
B木块与地面间的最大静摩擦力为：fBm=μGB=0.25×60N=15N；
用F=1N的水平拉力作用在木块B上，木块B受弹簧向右的弹力为8N．拉力为1N，共9N，小于最大静摩擦力，故静摩擦力为9N，向左；
A、B、木块A受到向左的弹力为8N，小于最大静摩擦力，故A不动，故静摩擦力为8N，向右；
故选AD
点评：本题关键是先判断出弹簧的弹力和最大静摩擦力，然后再分别对两个木块受力分析，运用平衡条件求解静摩擦力．
练习册系列答案
相关题目
如图所示，木块A、B用一轻弹簧相连，竖直放在木块C上，C静置于水平地面上，A、B、C的质量之比是1：2：3，设所有接触面都光滑．当沿水平方向迅速抽出木块C的瞬间，A、B的加速度分别是aA=
如图所示．木块A、B的质量分别是mA=5.0kg和mB=6.0kg，它们与水平地面之间的动摩擦因数均为μ=0.2，一轻弹簧原长为l0=10cm、劝度系数为k=400N/m．若用水平拉力F作用在木块B上，A、B在力F的作用下以共同的速度匀速运动，取g=10m/s2，求：
如图所示，木块A、B分别重50N和70N，它们与水平地面之间的动摩擦因数均为0.2，与A、B相连接的轻弹簧被压缩了5cm，系统置于水平地面上静止不动．已知弹簧的劲度系数为100N/m．现用F=7N的水平力作用在木块A上后，木块A所受摩擦力大小为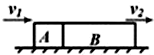
如图所示，木块A、B并排且固定在水平桌面上，A的长度是L，B的长度是3L，一颗子弹沿水平方向以速度v1射入A，以速度v2穿出B，子弹可视为质点，其运动视为匀变速直线运动，则子弹穿出A时的速度为（ ）