题目内容
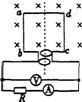
3．
如图所示，直线MN右侧有垂直纸面向外的匀强磁场，一导线框一半处于匀强磁场中，t=0时刻，框面与磁场垂直，现让线框以MN为轴匀速转动，并以开始运动的四分之一周期内的电流方向为正方向．则下列图象中能表示线框中感应电流随时间变化的是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 矩形金属线圈在匀强磁场中匀速转动，产生交流电．由于线圈始终有一半在磁场中切割产生感应电动势，由法拉第电磁感应定律求出感应电流大小，有楞次定律判断电流的方向．
解答 解：设线圈以MN为轴匀速转动，线圈始终有一半在磁场中产生感应电动势，图示位置线圈磁通量在最大，磁通量的变化率最小，即开始计时时，感应电流最小，在四分之一个周期内，磁通量减小，根据楞次定律可知，产生的感应电流沿adcba方向，转过四分之一周期后，cd边进入磁场，磁通量增大，根据楞次定律可知，产生的感应电流方向沿adcba方向，电流逐渐减小，故A正确，B错误
故选：A
点评 本题主要考查了线圈在磁场中产生感应电动势，关键是抓住线圈始终有一半在磁场中，明确计时时刻
练习册系列答案
相关题目
17．
绝缘水平桌面上放置一长直导线a，导线a的正上方某处放置另一长直导线b，两导线中均通以垂直纸面向里的恒定电流．现将导线b向右平移一小段距离，若导线a始终保持静止，则正确的是：（ ）
绝缘水平桌面上放置一长直导线a，导线a的正上方某处放置另一长直导线b，两导线中均通以垂直纸面向里的恒定电流．现将导线b向右平移一小段距离，若导线a始终保持静止，则正确的是：（ ）| A． | 导线b受到的安培力方向始终竖直向下 | |
| B． | 导线b受到的安培力逐渐减小 | |
| C． | 导线a对桌面的压力减小 | |
| D． | 导线a对桌面的摩擦力方向水平向左 |
如图所示，如果线圈abcd的面积是$\frac{11\sqrt{2}}{50}$m2，共100匝，线圈电阻为2Ω，外接电阻R=9Ω，匀强磁场的磁感应强度B=$\frac{1}{π}$T，当线圈以300r/min的转速绕垂直于磁场的轴匀速转动时．求：
11．
在竖直直角坐标系xOy平面内有一四分之一光滑圆柱体的截面OAB，半径为R．在x轴上的P点斜向左上方抛出一个小球（可视为质点）．小球的运动轨迹与圆柱体相切于D点，且到达y轴上的C点时速度与y轴垂直，OD与OB的夹角为60°，不计空气阻力，重力加速度大小为g．则小球在P点的速度大小为（ ）
在竖直直角坐标系xOy平面内有一四分之一光滑圆柱体的截面OAB，半径为R．在x轴上的P点斜向左上方抛出一个小球（可视为质点）．小球的运动轨迹与圆柱体相切于D点，且到达y轴上的C点时速度与y轴垂直，OD与OB的夹角为60°，不计空气阻力，重力加速度大小为g．则小球在P点的速度大小为（ ）| A． | $\sqrt{5Rg}$ | B． | 2$\sqrt{Rg}$ | C． | $\sqrt{3Rg}$ | D． | $\sqrt{2Rg}$ |
12．
如图所示，质量相同的A、B两小球用轻质细线悬挂在同一点O，在同一水平面上做匀速周运动．则下列说法错误的是（ ）
如图所示，质量相同的A、B两小球用轻质细线悬挂在同一点O，在同一水平面上做匀速周运动．则下列说法错误的是（ ）| A． | A的角速度一定比B的角速度大 | |
| B． | A的线速度一定比B的线速度大 | |
| C． | A的加速度一定比B的加速度大 | |
| D． | A所受细线的拉力一定比B所受的细线的拉力大 |