��Ŀ����
 ����ͼ��ʾ����O��ΪԲ�ģ���rΪ�뾶��Բ�������ύ��ֱ�Ϊa��b��c��d���ռ���һ��x����������ͬ����ǿ�糡��ͬʱ����O��̶�һ������Ϊ+Q�ĵ��ɣ������һ��������Ϊ-q�ļ����ɷ���c�㣬ǡ��ƽ�⣬��
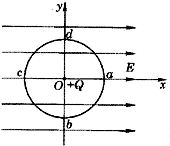
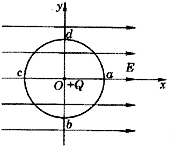
����ͼ��ʾ����O��ΪԲ�ģ���rΪ�뾶��Բ�������ύ��ֱ�Ϊa��b��c��d���ռ���һ��x����������ͬ����ǿ�糡��ͬʱ����O��̶�һ������Ϊ+Q�ĵ��ɣ������һ��������Ϊ-q�ļ����ɷ���c�㣬ǡ��ƽ�⣬����1����ǿ�糡�ij�ǿ��СEΪ���٣�
��2��a��d��ĺϳ�ǿ��С��Ϊ���٣�
��3�������O���������+Q���ߣ��ѵ���-q��c����x���Ƶ�a�㣬��糡�����Ĺ�����c��a�����ĵ��Ʋ
��������1�����ݵ�����c������ƽ����ʽ�������E��
��2������ʸ���ϳ�ԭ�������ad����ij�ǿ��С��
��3�����ݺ���������ʽ���糡�����Ĺ�������U=
�����Ʋ
��2������ʸ���ϳ�ԭ�������ad����ij�ǿ��С��
��3�����ݺ���������ʽ���糡�����Ĺ�������U=
| W |
| q |
����⣺��1������-q��c������ƽ�⣬����
k
=qE��
��ã�E=k
��
��2����a��ĺϳ�ǿ��СΪ
Ea=EQ+E=k
+k
=2k
d��ĺϳ�ǿΪ����+Q����ǿ�糡��ʸ�����ӣ���
Ed=
=
E=
k
��
��3���糡������W=-qE?2r=-2k
��
Uca=
=
=
��
�𣺣�1����ǿ�糡�ij�ǿ��СEΪk
��
��2��a�㳡ǿ��СΪ2k
��d��ĺϳ�ǿ��СΪ
k
��
��3�������O���������+Q���ߣ��ѵ���-q��c����x���Ƶ�a�㣬�糡�����Ĺ�Ϊ-2k
��
��c��a�����ĵ��Ʋ�Ϊ
��
k
| r2 |
��ã�E=k
| Q |
| r2 |
��2����a��ĺϳ�ǿ��СΪ
Ea=EQ+E=k
| Q |
| r2 |
| Q |
| r2 |
| Q |
| r2 |
d��ĺϳ�ǿΪ����+Q����ǿ�糡��ʸ�����ӣ���
Ed=
| E2+EQ2 |
| 2 |
| 2 |
| Q |
| r2 |
��3���糡������W=-qE?2r=-2k
| r |
Uca=
| Wca |
| q |
| 2qEr |
| q |
| 2kQ |
| r |
�𣺣�1����ǿ�糡�ij�ǿ��СEΪk
| Q |
| r2 |
��2��a�㳡ǿ��СΪ2k
| Q |
| r2 |
| 2 |
| Q |
| r2 |
��3�������O���������+Q���ߣ��ѵ���-q��c����x���Ƶ�a�㣬�糡�����Ĺ�Ϊ-2k
| r |
��c��a�����ĵ��Ʋ�Ϊ
| 2kQ |
| r |
������������Ҫ�����˿��ض��ɡ���ǿ�ĺϳ�ԭ�糡���������ص㼰�糡����������Ʋ�֮��Ĺ�ϵ���Ѷ����У�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
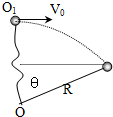 һ����Ϊm�ĺ�С����ϵ�ڳ�ΪR��������һ�ˣ�������һ�˹̶��ڿռ��O�㣬�ٶ����Dz����쳤�ġ����������Եģ����С���O������Ϸ���O��ľ���Ϊ
һ����Ϊm�ĺ�С����ϵ�ڳ�ΪR��������һ�ˣ�������һ�˹̶��ڿռ��O�㣬�ٶ����Dz����쳤�ġ����������Եģ����С���O������Ϸ���O��ľ���Ϊ