题目内容
设地球的质量为M且绕太阳做匀速圆周运动,有一质量为m的飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,一年后在D点飞船掠过地球上空,再过三个月,飞船在Q处掠过地球上空,如图所示,根据以上条件,求地球与太阳间的万有引力大小. (设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向,飞船到地球表面的距离远小于地球与太阳间的距离)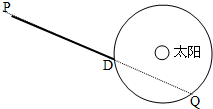

设一年时间为T,则三个月的时间为
T,三个月时间地球绕太阳转过90°角,
若地球到太阳的距离为r,则由几何关系得DQ=
r
a=
而DQ=PQ-PD=
a(
T)2-
aT2=
解得:r=r=
故所求F引 =M
=
答:地球与太阳间的万有引力大小为=
| 1 |
| 4 |
若地球到太阳的距离为r,则由几何关系得DQ=
| 2 |
a=
| F |
| m |
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
| 9FT2 |
| 32m |
解得:r=r=
9
| ||
| 64m |
故所求F引 =M
| 4π2r |
| T2 |
9
| ||
| 16m |
答:地球与太阳间的万有引力大小为=
9
| ||
| 16m |

练习册系列答案
相关题目
 (2007?深圳一模)设地球的质量为M且绕太阳做匀速圆周运动,有一质量为m的飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,一年后在D点飞船掠过地球上空,再过三个月,飞船在Q处掠过地球上空,如图所示,根据以上条件,求地球与太阳间的万有引力大小. (设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向,飞船到地球表面的距离远小于地球与太阳间的距离)
(2007?深圳一模)设地球的质量为M且绕太阳做匀速圆周运动,有一质量为m的飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,一年后在D点飞船掠过地球上空,再过三个月,飞船在Q处掠过地球上空,如图所示,根据以上条件,求地球与太阳间的万有引力大小. (设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向,飞船到地球表面的距离远小于地球与太阳间的距离)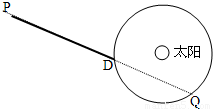 设地球的质量为M且绕太阳做匀速圆周运动,有一质量为m的飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,一年后在D点飞船掠过地球上空,再过三个月,飞船在Q处掠过地球上空,如图所示,根据以上条件,求地球与太阳间的万有引力大小. (设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向,飞船到地球表面的距离远小于地球与太阳间的距离)
设地球的质量为M且绕太阳做匀速圆周运动,有一质量为m的飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,一年后在D点飞船掠过地球上空,再过三个月,飞船在Q处掠过地球上空,如图所示,根据以上条件,求地球与太阳间的万有引力大小. (设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向,飞船到地球表面的距离远小于地球与太阳间的距离)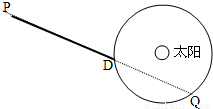 设地球的质量为M且绕太阳做匀速圆周运动,有一质量为m的飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,一年后在D点飞船掠过地球上空,再过三个月,飞船在Q处掠过地球上空,如图所示,根据以上条件,求地球与太阳间的万有引力大小. (设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向,飞船到地球表面的距离远小于地球与太阳间的距离)
设地球的质量为M且绕太阳做匀速圆周运动,有一质量为m的飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,一年后在D点飞船掠过地球上空,再过三个月,飞船在Q处掠过地球上空,如图所示,根据以上条件,求地球与太阳间的万有引力大小. (设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向,飞船到地球表面的距离远小于地球与太阳间的距离)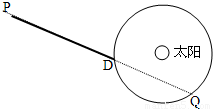 设地球的质量为M且绕太阳做匀速圆周运动,有一质量为m的飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,一年后在D点飞船掠过地球上空,再过三个月,飞船在Q处掠过地球上空,如图所示,根据以上条件,求地球与太阳间的万有引力大小. (设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向,飞船到地球表面的距离远小于地球与太阳间的距离)
设地球的质量为M且绕太阳做匀速圆周运动,有一质量为m的飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,一年后在D点飞船掠过地球上空,再过三个月,飞船在Q处掠过地球上空,如图所示,根据以上条件,求地球与太阳间的万有引力大小. (设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向,飞船到地球表面的距离远小于地球与太阳间的距离)