题目内容
一底面半径为R的半圆柱形透明体的折射率为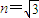 ,横截面如图所示,O表示半圆柱形截面的圆心.一束极窄的光线在横截面内从AOB边上的A点以60°的入射角入射,求:该光线从进入透明体到第一次离开透明体时,共经历的时间(已知真空中的光速为c,
,横截面如图所示,O表示半圆柱形截面的圆心.一束极窄的光线在横截面内从AOB边上的A点以60°的入射角入射,求:该光线从进入透明体到第一次离开透明体时,共经历的时间(已知真空中的光速为c,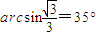 ;计算结果用R、n、c表示).
;计算结果用R、n、c表示).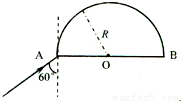
【答案】分析:由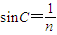 求出临界角.入射角i=60°,由折射定律n=
求出临界角.入射角i=60°,由折射定律n=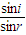 求出光线从AB射入透明体的折射角r,判断光线在圆弧上能否发生全反射,作出光路图,由几何知识求解光线在透明体内的路程s,光线在透明体的速度为v=
求出光线从AB射入透明体的折射角r,判断光线在圆弧上能否发生全反射,作出光路图,由几何知识求解光线在透明体内的路程s,光线在透明体的速度为v=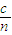 ,通过的时间为t=
,通过的时间为t=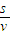 .
.
解答:设此透明物体的临界角为C,
依题意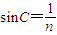 =
=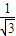 ,所以C=35°
,所以C=35°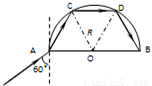
当入射角为i=60°时,由折射定律n=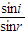 得
得
得到折射角:r=30°
即此时光线折射后射到圆弧上的C点,在C点的入射角为60°,大于临界角,会发生全反射,往后光线水平反射至圆弧上的D点并在D点发生全反射,再反射至B点,从B点第一次射出.在透明体内的路径长为:s=3R 光在透明体内的速度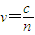
经历的时间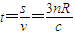
答:该光线从进入透明体到第一次离开透明体时,共经历的时间为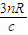 .
.
点评:画出光路图是基础,判断能否发生全反射是关键.运用几何知识求出光线在透明体通过的总路程.
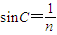 求出临界角.入射角i=60°,由折射定律n=
求出临界角.入射角i=60°,由折射定律n=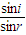 求出光线从AB射入透明体的折射角r,判断光线在圆弧上能否发生全反射,作出光路图,由几何知识求解光线在透明体内的路程s,光线在透明体的速度为v=
求出光线从AB射入透明体的折射角r,判断光线在圆弧上能否发生全反射,作出光路图,由几何知识求解光线在透明体内的路程s,光线在透明体的速度为v=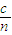 ,通过的时间为t=
,通过的时间为t=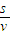 .
.解答:设此透明物体的临界角为C,
依题意
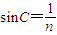 =
=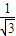 ,所以C=35°
,所以C=35°
当入射角为i=60°时,由折射定律n=
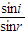 得
得得到折射角:r=30°
即此时光线折射后射到圆弧上的C点,在C点的入射角为60°,大于临界角,会发生全反射,往后光线水平反射至圆弧上的D点并在D点发生全反射,再反射至B点,从B点第一次射出.在透明体内的路径长为:s=3R 光在透明体内的速度
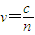
经历的时间
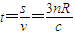
答:该光线从进入透明体到第一次离开透明体时,共经历的时间为
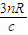 .
.点评:画出光路图是基础,判断能否发生全反射是关键.运用几何知识求出光线在透明体通过的总路程.

练习册系列答案
相关题目
