题目内容
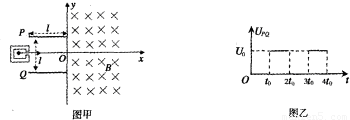
如图甲所示的坐标系Oxy，一、四象限内有磁感应强度为B、方向垂直于Oxy平面向里的匀强磁场，两平行极板P、Q垂直于y轴且关于x轴对称，极板右端位于y轴上，极板长度和板间距均为l，P，Q极板间加如图乙所示的电压．位于极板在左侧的粒子源沿x轴向右连续发射速度相同、重力不计的带正电粒子，已知t=tp时刻（UPQ=UO）发出的粒子恰好在2tO时刻经极板边缘飞出电场，不考虑粒子间相互影响及返回板间的情况，不考虑极板边缘的影响，上述B、l、UO、tO均为已知量．（1）求粒子的比荷q/m；
（2）若t=0时刻从粒子源发出的粒子在进入磁场后到达y轴上的M点，求M点的坐标；
（3）若t时刻（0＜t＜tO）从粒子源发出的粒子在进入磁场后到达y轴上的N点，设N点与第（2）问中M点之间的距离为D，试求D与t的函数关系．
【答案】分析：（1）t=t时刻进入两极板的带电粒子在电场中做类平抛运动．由题知道x方向位移为l，y方向位移为
运用运动的分解，根据牛顿第二定律和运动学公式求解粒子的比荷q/m．
（2）若t=0时刻发出的粒子在电场中做匀速直线运动，进入磁场后做匀速圆周运动，根据洛伦兹力提供向心力求出半径，即可求出M点坐标．
（3）t时刻发出的粒子，在电场中运动的总时间为t，粒子先做匀速运动，速度为v，运动时间为（t-t），再做类平抛运动，后在磁场中做匀速圆周运动，画出轨迹，根据几何关系即可求解．
解答：解：（1））t=t时刻进入两极板的带电粒子在电场中做类平抛运动，运动时间为t，则
竖直方向：
①
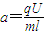②
①②联立解得：
③
（2）t=0时刻发出的粒子在电场中做匀速直线运动，速度大小为
④
进入磁场后做匀速圆周运动，设半径为R1
根据洛伦兹力提供向心力得：
⑤，
③④⑤联立得：
，⑥
故M点的坐标为（0，
）
（3）t时刻发出的粒子，在电场中运动的总时间为t，粒子先做匀速运动，速度为v，运动时间为（t-t），再做类平抛运动，运动时间为t．设粒子离开电场时的偏转位移为y，偏转角度为θ，进入磁场时的速度为v，在磁场中的轨迹半径为R2．如图所示，
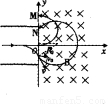
根据几何关系有：D+2R2cosθ=2R1+y ⑦
⑧
⑨
⑦⑧⑨联立得：D=y ⑩
又
且有①式得：
（11）
⑩（11）联立得：
答：（1）粒子的比荷
；
（2）M点的坐标（0，
）；
（3）D与t的函数关系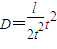
．
点评：本题考查带电粒子在匀强磁场和匀强电场中的运动，要掌握住半径公式、周期公式，画出粒子的运动轨迹后，几何关系就比较明显了．
运用运动的分解，根据牛顿第二定律和运动学公式求解粒子的比荷q/m．（2）若t=0时刻发出的粒子在电场中做匀速直线运动，进入磁场后做匀速圆周运动，根据洛伦兹力提供向心力求出半径，即可求出M点坐标．
（3）t时刻发出的粒子，在电场中运动的总时间为t，粒子先做匀速运动，速度为v，运动时间为（t-t），再做类平抛运动，后在磁场中做匀速圆周运动，画出轨迹，根据几何关系即可求解．
解答：解：（1））t=t时刻进入两极板的带电粒子在电场中做类平抛运动，运动时间为t，则
竖直方向：
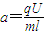① ②①②联立解得：
③（2）t=0时刻发出的粒子在电场中做匀速直线运动，速度大小为
④进入磁场后做匀速圆周运动，设半径为R1
根据洛伦兹力提供向心力得：
⑤，③④⑤联立得：
，⑥故M点的坐标为（0，
）（3）t时刻发出的粒子，在电场中运动的总时间为t，粒子先做匀速运动，速度为v，运动时间为（t-t），再做类平抛运动，运动时间为t．设粒子离开电场时的偏转位移为y，偏转角度为θ，进入磁场时的速度为v，在磁场中的轨迹半径为R2．如图所示，
根据几何关系有：D+2R2cosθ=2R1+y ⑦
⑧ ⑨⑦⑧⑨联立得：D=y ⑩
又
且有①式得： （11）⑩（11）联立得：
答：（1）粒子的比荷
；（2）M点的坐标（0，
）；（3）D与t的函数关系
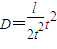．点评：本题考查带电粒子在匀强磁场和匀强电场中的运动，要掌握住半径公式、周期公式，画出粒子的运动轨迹后，几何关系就比较明显了．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
方向的宽度OA=
cm，
方向无限制，磁感应强度B0=1×10-4T。现有一比荷为
=2×1011C
/kg的正离子以某一速度从O点射入磁场，α=60°，离子通过磁场后刚好从A点射出。
方向的宽度OA=20
cm，
方向无限制，磁感应强度B0=1×10-4T。现有一比荷为q/m=2×1011C/kg的正离子以某一速度从O点射入磁场，α=60°，离子通过磁场后刚好从A点射出。
方向的宽度OA=
cm，
方向无限制，磁感应强度B0=1×10-4T。现有一比荷为
=2×1011C/kg的正离子以某一速度从O点射入磁场，α=60°，离子通过磁场后刚好从A点射出。