题目内容
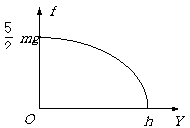
跳水运动员从高于水面H＝10m的跳台自由落下，身体笔直且与水面垂直．假设运动员的质量m＝50kg，其体型可等效为一长度L＝1.0m、直径d＝0.30m的圆柱体，略去空气阻力．运动员落水后，水的等效阻力f作用于圆柱体的下端面，f的量值随落水深度Y变化的函数曲线如图所示． 该曲线可近似看作椭圆的一部分，该椭圆的长、短轴分别与坐标轴OY和Of重合．运动员入水后受到的浮力F＝ρgV （V是排开水的体积）是随着入水深度线性增加的．已知椭圆的面积公式是S＝πab，水的密度ρ＝1.0×103kg/m3， g取10m/s2．
试求：
（1）运动员刚入水时的速度；
（2）运动员在进入水面过程中克服浮力做的功；
（3）为了确保运动员的安全，水池中水的深度h至少应等于多少？
解答：（1）
(2分）
（2）浮力做功分为两个阶段，运动员进入水面为第一阶段，水的浮力线性增加，其做功为：
… 
(2分）
WF1 ＝ -353.25 J (1分）
（3）设水深为h，第二阶段浮力是恒力，其所做的功
…
(2分）
水的阻力做功为图中曲线与横轴所围的面积：
＝
… 
(2分）
运动员的始、末状态的速度均为零，对整个过程应用动能定理：
WG ＋WF1＋ WF2＋ Wf ＝0 … 
(2分）
将WG ＝ mg(H ＋h）及、、式代入式：
＝0， (2分）
代入数据解得至少水深为 h＝ 4.51m (1分）
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
相关题目
（2012?长宁区一模）跳水运动员从高于水面H=10m的跳台自由落下，身体笔直且与水面垂直．假设运动员的质量m=50kg，其体型可等效为一长度L=1.0m、直径d=0.30m的圆柱体，略去空气阻力．运动员落水后，水的等效阻力f作用于圆柱体的下端面，f的量值随落水深度Y变化的函数曲线如图所示． 该曲线可近似看作椭圆的一部分，该椭圆的长、短轴分别与坐标轴OY和Of重合．运动员入水后受到的浮力F=ρgV （V是排开水的体积）是随着入水深度线性增加的．已知椭圆的面积公式是S=πab，水的密度ρ=1.0×103kg/m3，g取10m/s2．
