题目内容
已知抛物线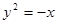 与直线
与直线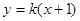 相交于A、B 两点.
相交于A、B 两点.
(1)求证: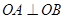 ;
;
(2)当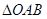 的面积等于
的面积等于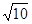 时,求
时,求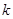 的值.
的值.
【答案】
(1)见解析;(2)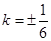 .
.
【解析】
试题分析:(1)通过证明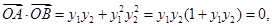 得到
得到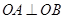 .
.
(2)注意到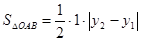 ,因此由
,因此由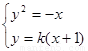 得
得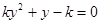 .应用韦达定理确定
.应用韦达定理确定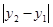 ,利用
,利用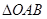 的面积等于
的面积等于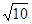 ,建立
,建立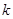 的方程.
的方程.
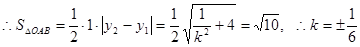 . 13分
. 13分
试题解析:(1)证明:设 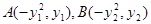 ,
,
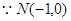 ,
,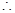
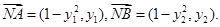
由A,N,B共线,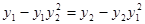 ,
,
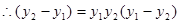 ,
,
又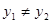 ,
,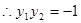 ,
,
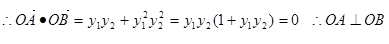 .
6分
.
6分
(2)解:
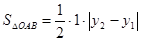 , 由
, 由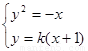 得
得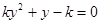 .
.
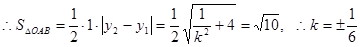 . 13分
. 13分
考点:平面向量的坐标运算,直线与抛物线的位置关系,韦达定理.

练习册系列答案
相关题目