Question

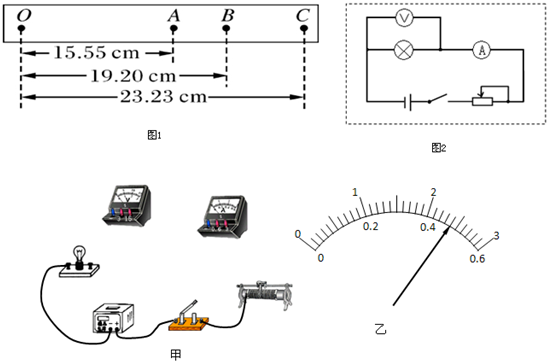
如图所示为一次记录小车运动情况的纸带，图中A、B、C、D、E、F、G为相邻的记数点，相邻记数点的时间间隔T=0.1s．
（1）计算运动物体在E、F点的瞬时速度（保留三位有效数字）．

各个点	B	C	D	E	F
v/m?s-1	0.165	0.214	0.263

（2）在坐标系中作出小车的v-t图线．
（3）由图线得到小车的加速度为

 

m/s²．（保留两位有效数字）

Answer 1

分析：根据匀变速直线运动中间时刻的速度等于该过程中的平均速度，可以求出打纸带上某点时小车的瞬时速度大小，根据描点法作出速度-时间图象，图象的斜率表示加速度．

解答：解：（1）根据匀变速直线运动中间时刻的速度等于该过程中的平均速度，得：
vE=

xDF

2T

=

0.0288+0.0339

0.2

=0.314m/s
vF=

xEG

2T

=

0.0387+0.0339

0.2

=0.363m/s
（2）根据描点法作出速度-时间图象，如图所示：
（3）根据图象得：
a=

△v

△t

=

0.35-0.12

0.45

=0.51m/s2
故答案为：（1）0.314；0.363；（2）如图所示；（3）0.51

点评：纸带处理是力学实验中的常见问题．我们要结合匀变速直线运动规律去求解．要注意实验中的单位问题．