题目内容
 如图所示,物体A、B通过细绳及轻质弹簧连接在轻滑轮两侧,物体A、B的质量都为m.开始时细绳伸直,用手托着物体A使弹簧处于原长且A与地面的距离为h,物体B静止在地面上.放手后物体A下落,与地面即将接触时速度大小为v,此时物体B对地面恰好无压力,则下列说法中正确的是
如图所示,物体A、B通过细绳及轻质弹簧连接在轻滑轮两侧,物体A、B的质量都为m.开始时细绳伸直,用手托着物体A使弹簧处于原长且A与地面的距离为h,物体B静止在地面上.放手后物体A下落,与地面即将接触时速度大小为v,此时物体B对地面恰好无压力,则下列说法中正确的是
- A.弹簧的劲度系数为

- B.此时弹簧的弹性势能等于

- C.此时物体B的速度大小也为v
- D.此时物体A的加速度大小为g,方向竖直向上
A
分析:由题,物体B对地面恰好无压力时,物体A下落高度为h,则知此时弹簧所受的拉力大小等于B的重力mg,弹簧伸长的长度为h,由胡克定律F=kx求解弹簧的劲度系数.A与弹簧组成的系统机械能守恒,可求解求得弹簧的弹性势能.此时物体B的速度为零.根据牛顿第二定律求出A的加速度.
解答:A、由题可知,此时弹簧所受的拉力大小等于B的重力,即F=mg,弹簧伸长的长度为x=h,由F=kx得,k= .故A正确.
.故A正确.
B、A与弹簧组成的系统机械能守恒,则有:
mgh=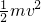 +Ep,则弹簧的弹性势能:Ep=mgh-
+Ep,则弹簧的弹性势能:Ep=mgh-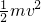 .故B错误.
.故B错误.
C、物体B对地面恰好无压力时,此时B的速度恰好为零.故C错误.
D、根据牛顿第二定律对A有:F-mg=ma,得a=0.故D错误.
故选A
点评:本题是含有弹簧的问题,运用胡克定律、机械能守恒和牛顿第二定律进行研究,关键要抓住物体B对地面恰好无压力,确定出弹簧的弹力.
分析:由题,物体B对地面恰好无压力时,物体A下落高度为h,则知此时弹簧所受的拉力大小等于B的重力mg,弹簧伸长的长度为h,由胡克定律F=kx求解弹簧的劲度系数.A与弹簧组成的系统机械能守恒,可求解求得弹簧的弹性势能.此时物体B的速度为零.根据牛顿第二定律求出A的加速度.
解答:A、由题可知,此时弹簧所受的拉力大小等于B的重力,即F=mg,弹簧伸长的长度为x=h,由F=kx得,k=
 .故A正确.
.故A正确.B、A与弹簧组成的系统机械能守恒,则有:
mgh=
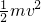 +Ep,则弹簧的弹性势能:Ep=mgh-
+Ep,则弹簧的弹性势能:Ep=mgh-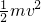 .故B错误.
.故B错误.C、物体B对地面恰好无压力时,此时B的速度恰好为零.故C错误.
D、根据牛顿第二定律对A有:F-mg=ma,得a=0.故D错误.
故选A
点评:本题是含有弹簧的问题,运用胡克定律、机械能守恒和牛顿第二定律进行研究,关键要抓住物体B对地面恰好无压力,确定出弹簧的弹力.

练习册系列答案
相关题目
如图所示,物体A和B相对静止,以共同的速度沿斜面匀速下滑,则( )
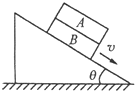

| A、A、B间无摩擦力的作用 | B、B受到滑动摩擦力的大小为(mA+mB)gsinθ | C、B受到静摩擦力的大小为mAgsinθ | D、A物体受到的合力沿斜面向下 |
 如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中,则( )
如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中,则( ) 如图所示,物体A、B叠放在倾角θ=37°的斜面上,并通过跨过光滑滑轮的细线相连,细线与斜面平行.两物体的质量分别mA=2kg,mB=1kg,A、B间动摩擦因数μ1=0.1,B与斜面间的动摩擦因数μ2=0.2,问:为使A能平行于斜面向下做匀速运动,应对A施加一平行于斜面向下的多大的拉力?
如图所示,物体A、B叠放在倾角θ=37°的斜面上,并通过跨过光滑滑轮的细线相连,细线与斜面平行.两物体的质量分别mA=2kg,mB=1kg,A、B间动摩擦因数μ1=0.1,B与斜面间的动摩擦因数μ2=0.2,问:为使A能平行于斜面向下做匀速运动,应对A施加一平行于斜面向下的多大的拉力? 如图所示,物体A和B一起沿斜面匀速下滑,则物体A受到的力是( )
如图所示,物体A和B一起沿斜面匀速下滑,则物体A受到的力是( ) 如图所示,物体A、B 叠放在光滑的水平地面上mA=1kg,mB=2kg,A、B问最大静摩擦力为6N,用水平推力F推A,为使A、B不产生相对滑动,F最大为
如图所示,物体A、B 叠放在光滑的水平地面上mA=1kg,mB=2kg,A、B问最大静摩擦力为6N,用水平推力F推A,为使A、B不产生相对滑动,F最大为