题目内容
[物理一选修3-5](1)雷蒙德?戴维斯因研究来自太阳的电子中微子 (ve)而获得了2002年度诺贝尔物理学奖.他在探测中微子过程中所涉及的一个核反应方程式为:ve+
 →
→ +
+ ,己如
,己如 核的质量为36.95658u;
核的质量为36.95658u; 核的质量为36.95691u,
核的质量为36.95691u, 的质量为0.00055u,1u质量对应的能量为931.5MeV.根据以上数据,可以判断参与上述反应的电子中微子的最小能量为______MeV
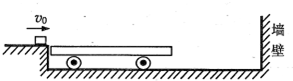
的质量为0.00055u,1u质量对应的能量为931.5MeV.根据以上数据,可以判断参与上述反应的电子中微子的最小能量为______MeV(2)如图所示,质量为m=1kg的滑块,以v=5m/s的水平初速度滑上静止在光滑水平面上的平板小车,小车质量M=4kg,小车与右边的墙壁发生弹性碰撞后以等大反向的速度被反弹回来,在小车与墙壁碰撞前后各有一次滑块和小车相对静止的状态,求:
①与墙壁碰撞前滑块与小车的共同速度v1大小;
②与墙壁碰撞后滑块与小车的共同速度v2大小.

【答案】分析:(1)根据题意可知该核反应过程中质量增加,因此需要提供能量,根据质能方程求出反应所需能量,然后根据能量的守恒即可求出中微子的最小能量.
(2)选择正确的研究对象,根据动量守恒定律求解问题.
解答:解:(1)反应过程需要能量为:E=mc2=(36.95691u+0.00055u-36.95658u)c2
根据l u质量对应的能量为931.5MeV,得:E≈0.82MeV,所以中微子的能量最小为0.82MeV,
(2)①根据动量守恒定律:mv=(m+M)v1

②根据动量守恒定律Mv1-mv1=(m+M)v2

故答案为:(1)0.82
(2)①与墙壁碰撞前滑块与小车的共同速度v1大小是1m/s;
②与墙壁碰撞后滑块与小车的共同速度v2大小是0.6m/s.
点评:(1)本题考查了能量守恒在原子物理知识中的应用,要解答这类问题关键是在计算上不要出错.
(2)根据动量守恒列出等式求解是常见的问题,要注意动量的方向.
(2)选择正确的研究对象,根据动量守恒定律求解问题.
解答:解:(1)反应过程需要能量为:E=mc2=(36.95691u+0.00055u-36.95658u)c2
根据l u质量对应的能量为931.5MeV,得:E≈0.82MeV,所以中微子的能量最小为0.82MeV,
(2)①根据动量守恒定律:mv=(m+M)v1

②根据动量守恒定律Mv1-mv1=(m+M)v2

故答案为:(1)0.82
(2)①与墙壁碰撞前滑块与小车的共同速度v1大小是1m/s;
②与墙壁碰撞后滑块与小车的共同速度v2大小是0.6m/s.
点评:(1)本题考查了能量守恒在原子物理知识中的应用,要解答这类问题关键是在计算上不要出错.
(2)根据动量守恒列出等式求解是常见的问题,要注意动量的方向.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
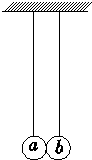 [物理一选修3-5]如图,大小相同的摆球a和b的质量分别为m和3m,摆长相同,并排悬挂,平衡时两球刚好接触.现摆球a向左拉开一小角度后释放.若两球的碰撞是弹性的,下列判断正确的是( )
[物理一选修3-5]如图,大小相同的摆球a和b的质量分别为m和3m,摆长相同,并排悬挂,平衡时两球刚好接触.现摆球a向左拉开一小角度后释放.若两球的碰撞是弹性的,下列判断正确的是( )| A、第一次碰撞后的瞬间,两球的速度大小相等 | B、第一次碰撞后的瞬间,两球的动量大小相等 | C、第一次碰撞后,两球的最大摆角不相同 | D、发生第二次碰撞时,两球在各自的平衡位置的右侧 |
 [物理一选修3-5]
[物理一选修3-5]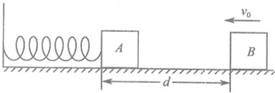 [物理--一选修3-5]
[物理--一选修3-5]