题目内容
光滑曲面与竖直平面的交线是抛物线，如图所示，抛物线的方程是y=x2，其下半部分处在一个水平方向的匀强磁场中，磁场的上边界是y=a的直线（虚线所示），一个小金属块从抛物线上y=b（b＞a）处以初速度v沿抛物线下滑，假设抛物线足够长，则金属块在曲面上滑动的过程中产生的焦耳热总量是（ ）
A．mgb B．
mv2
C．mg（b-a） D．mg（b-a）+
mv2
答案：D
解析：
解析：
小金属块每次沿抛物线曲面滑入磁场过程中，由于电磁感应，机械能通过磁场力做功转化为焦耳热，则小金属块滑离磁场的高度越来越小．所以，小金属块的运动最终收敛为恰好不能离开磁场，即以上边界直线所在处为最高点的往复运动．据能量守恒定律，可得：
|
，故D项正确．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
光滑曲面与竖直平面的交线是抛物线，如图所示，抛物线的方程是y=x2，下半部处在一个水平方向的匀强磁场中，磁场的上边界是y=a的直线（图中的虚线所示）．一个小金属块从抛物线上y=b（b＞a）外以速度v沿抛物线下滑．假设抛物线足够长，金属块沿抛物线下滑后产生的焦耳热总量是（ ）
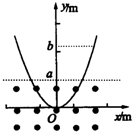光滑曲面与竖直平面的交线是抛物线，抛物线的方程是y=x2，如图所示．下半部处在一个水平方向的匀强磁场中，磁场的上边界是y=a的直线（图中的虚线所示）．一个小金属块从抛物线上y=b（b＞a）处从静止开始沿抛物线下滑．假设抛物线足够长，金属块沿抛物线下滑后产生的焦耳热总量是（ ）| A、mgb | ||
| B、mga | ||
| C、mg（b-a） | ||
D、mg（b-a）+
|
光滑曲面与竖直平面的交线是抛物线，如图所示，抛物线的方程是y=x2，下半部处在一个水平方向的匀强磁场中，磁场的上边界是y=a的直线（图中虚线所示），一个小金属环从抛物线上y=b（y>a）处以速度v沿抛物线下滑，假设抛物线足够长，金属环沿抛物线下滑后产生的焦耳热总量是（ ）
| A．mgb | B． |
| C．mg(b－a) | D． |
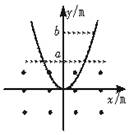
光滑曲面与竖直平面的交线是抛物线，如图6所示，抛物线的方程是y＝x2，下半部处在一个水平方向的匀强磁场中，磁场的上边界是y＝a的直线（图中的虚线所示）．一个小金属块从抛物线上y＝b（b＞a）处以速度v沿抛物线下滑．假设抛物线足够长，金属块沿抛物线下滑后产生的焦耳热总量是
|
A．mgb B．
mv2?C．mg（b－a） D．mg（b－a）＋ mv2
