题目内容
（2008?虹口区二模）如图所示，质量为m的小球A穿在绝缘细杆上，杆的倾角为α，小球A带正电，电量为q，在杆上B点处固定一个电量为Q的正电荷．将A由距B竖直高度为H处无初速释放，小球A下滑过程中电量不变．不计A与细杆间的摩擦，整个装置处在真空中．已知静电力恒量k和重力加速度g，求：（1）A球刚释放时的加速度．
（2）当A球的动能最大时，求此时A球与B点的距离．
分析：（1）对A球受力分析，受到重力、支持力和静电斥力，根据牛顿第二定律求加速度；
（2）小球A先加速下滑，当静电斥力等于重力的下滑分量时，小球速度最大，之后减速下降，再加速返回，减速返回到最高点，完成一次振动，即在平衡位置速度最大．
（2）小球A先加速下滑，当静电斥力等于重力的下滑分量时，小球速度最大，之后减速下降，再加速返回，减速返回到最高点，完成一次振动，即在平衡位置速度最大．
解答：解：（1）由牛顿第二定律得：mgsinα-F=ma，
由库仑定律得：F=k
，由几何知识得：r=
，
解得：a=gsinα-
；
（2）当A球所受合力为零，加速度为零时，速度最大，动能最大．
设此时AB间距离为L，由平衡条件得：mgsinα=k
，
解得：L=
；
答：（1）A球刚释放时的加速度为gsinα-
．
（2）当A球的动能最大时，A球与B点的距离为
．
由库仑定律得：F=k
| r2 |
| H |
| sinα |
解得：a=gsinα-
| kQqsin2α |
| mH2 |
（2）当A球所受合力为零，加速度为零时，速度最大，动能最大．
设此时AB间距离为L，由平衡条件得：mgsinα=k
| L2 |
解得：L=
|
答：（1）A球刚释放时的加速度为gsinα-
| kQqsin2α |
| mH2 |
（2）当A球的动能最大时，A球与B点的距离为
|
点评：本题关键对小球A受力分析，然后根据牛顿第二定律求解加速度，根据力与速度关系分析小球A的运动情况．
练习册系列答案
阅读快车系列答案
相关题目
（2008?虹口区二模）如图所示是用转动八面镜法测光速的实验示意图，图中S为发光点，T是望远镜，平面镜O与凹面镜B构成了反射系统．八面镜M距反射系统的距离为AB=L（L可长达几十千米），且远大于OB以及S和T到八面镜的距离．现使八面镜转动起来，并缓慢增大其转速，当转动频率（1秒内转过的圈数）达到f0时（可认为是匀速转动），恰能在望远镜中第一次看见发光点S，由此测出光速c．根据题中所测量的物理量得到光速c的表达式正确的是 （ ）
（2008?虹口区二模）如图所示为起重机沿竖直方向提起的过程中重物运动的速度-时间图象，则该过程中起重机的输出功率最接近下图中的（ ）
（2008?虹口区二模）如图所示，一列简谐横波沿x轴负方向传播，振幅A=4cm．在t=0时刻，平衡位置相距5cm的两质点a、b的位移分别是2cm、-2cm，它们的运动方向都沿y轴的负方向，据此可以推断（ ）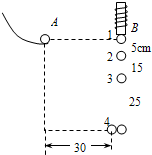
（2008?虹口区二模）如图所示，是利用闪光照相研究平抛运动的示意图，小球A由斜槽滚下，从桌边缘水平抛出，当它恰好离开桌边缘时，小球B也同时下落，闪光频率为10Hz的闪光器拍摄的照片中B球有四个像，像间距离已在图中标出，单位为cm，两球恰在位置4相碰．