��Ŀ����
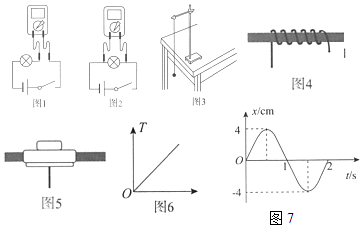
����Ŀ����ͼ����Ե�ֲڵ���ֱƽ��MN���ͬʱ�������ֱ����ǿ�糡����ǿ�ų����糡����ˮƽ���ң��糡ǿ�ȴ�СΪE���ų�����ֱֽ�����⣬�Ÿ�Ӧǿ�ȴ�СΪB��һ����Ϊm�������Ϊq�Ĵ������С�����A���ɾ�ֹ��ʼ��MN�»�������C��ʱ�뿪MN�������˶���A��C��������Ϊh���������ٶ�Ϊg��
��1����С�����˶���C��ʱ���ٶȴ�Сvc��
��2����С�����A���˶���C������п˷�Ħ�������Ĺ�Wf��
��3����D��ΪС�����ڵ糡�������������������������˶��������ٶ�����λ�ã���С�����˶���D��ʱ��ȥ�ų����˺�С��������˶���ˮƽ�����ϵ�P�㣮��֪С������D��ʱ���ٶȴ�СΪvD �� ��D���˶���P���ʱ��Ϊt����С�����˶���P��ʱ�ٶȵĴ�Сvp ��
���𰸡�
��1��
�⣺С������MN�˶����̣�ˮƽ������������
qvB+N=qE
С������C���뿪MNʱ
N=0
��� vc= ![]()
��С�����˶���C��ʱ���ٶȴ�СvcΪ ![]()
��2��
�⣺�ɶ��ܶ���
mgh��Wf= ![]() ��0
��0
��� Wf=mgh�� ![]()
��С�����A���˶���C������п˷�Ħ�������Ĺ�WfΪmgh�� ![]() ��
��
��3��
�⣺��ͼ��

С�����ٶ����ʱ���ٶȷ�����糡���������ĺ�������ֱ��
��ȥ�ų���С���齫����ƽ���˶�����Ч���ٶ�Ϊg�䣬
g��= ![]()
�� ![]()
��� ![]()
��С�����˶���P��ʱ�ٶȵĴ�СvpΪ ![]()
���������������Ĺؼ��Ƿ������С������˶����̣�����MN����ʱ��С������MN���������Ϊ�㣬�ڳ�ȥ�ų���С���齫����ƽ���˶������ݻ���IJ�ͬ���˶���������⼴�ɣ�
�����㾫�����������⣬������Ҫ�˽�ܶ������ۺ�Ӧ��(Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ��)��