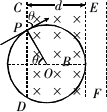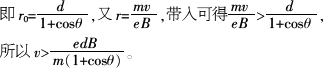Question

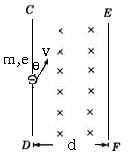
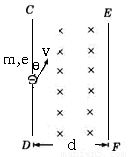
如图所示，真空中狭长区域内分布有磁感应强度为B的匀强磁场，方向垂直纸面向里，区域的宽度为d，CD、EF为区域的边界．现有一束电子(电荷量为e，质量为m)以速率v从CD侧垂直于磁场与CD边成角射入，为使电子能从另一侧EF射出，则电子的速率v应满足什么条件．

Answer 1

答案：
解析：

讲析：这是个临界问题，关键是求出刚好穿出磁场时，速度等于多少，求该速度的关键是画出运动的临界情况的轨迹． 　　电子从P点入射后受f洛作用将做顺时针方向的匀速圆周运动，其轨迹是一段圆弧，先画出如图所示的整个圆，根据题意，可在我们已画好的圆上确定入射点P，画出磁场的左边界CD；假定磁场的右边界可移动，我们再画一条与CD边平行的直线EF(磁场的右边界)，并逐渐向圆靠近，则当EF与圆相切时，就是电子能从EF射出的临界情况． 　　设此时圆弧与右边相切时的半径为r0，依题意，磁场宽度一定，故只有当圆的半径r＞r0时才能满足要求．根据圆的几何知识，可得r0＋r0cos＝d， 　　 　　点评：对于直线型边界的情况，先画出圆后，可以根据题意调整边界线的位置来找长度间的几何关系．