题目内容
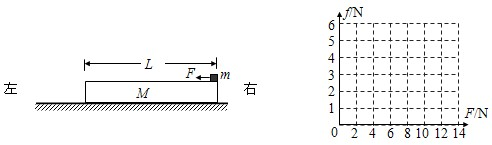
如图，质量M=1kg的木板静止在水平面上，质量m=1kg、大小可以忽略的铁块静止在木板的右端。设最大摩擦力等于滑动摩擦力，已知木板与地面间的动摩擦因数μ1=0.1，铁块与木板之间的动摩擦因数μ2=0.4，取g=10m/s2．现给铁块施加一个水平向左的力F．
1.若力F恒为8N，经1s铁块运动到木板的左端。求：木板的长度
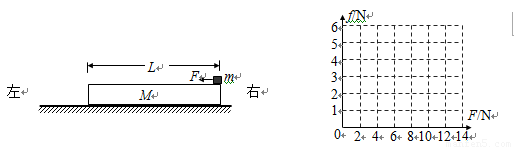
2.若力F从零开始逐渐增加，且木板足够长。试通过分析与计算，在图中作出铁块受到的摩擦力f随力F大小变化的图象
1.1ｍ
2.见解析
解析:（1）铁块的受力如图，由牛顿第二定律：
……①
木板的受力如图，由牛顿第二定律：
……②
设木板的长度为Ｌ，经时间t铁块运动到木板的左端，则
……③ 
……④
又：
……⑤ 联立①②③④⑤解得：Ｌ=1ｍ……⑥
（2）（i）当
时，系统没有被拉动，静摩擦力与外力成正比，即：f=F
（ii）当
时，如果M、m相对静止，铁块与木板有相同的加速度a，则：
……⑦
……⑧
解得：
……⑨
此时：
，也即
……⑩
所以：当
时，
……11
（iii）当
时，M、m相对滑动，此时铁块受到的摩擦力为：
f—F图象如图所示
练习册系列答案
同步拓展阅读系列答案
相关题目
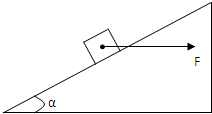如图，质量m=1kg的物体在F=20N水平向右的拉力作用下由静止开始沿足够长的斜面向上滑动，斜面固定不动且与水平方向成α=37°角，物体与斜面之间的动摩擦因数μ=0.25，拉力F作用物体2s后撤去．
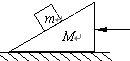如图，质量m=1kg的物块放在倾角为θ的斜面上，斜面体质量M=2kg，斜面与物块间的动摩擦因数μ=0.2，地面光滑，θ=37°，现对斜面体施一水平推力F，要使物体m相对斜面静止，力F应为多大？（ g=10m/s2，设物体与斜面的最大静摩擦力等于滑动摩擦力）
