题目内容
地球绕太阳作圆周运动的半径为r1、周期为T1;月球绕地球作圆周运动的半径为r2、周期为T2.万有引力常量为G,不计周围其它天体的影响,则根据题中给定条件AC( )A.能求出地球的质量
B.表达式
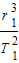 =
=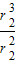 成立
成立C.能求出太阳与地球之间的万有引力
D.能求出地球与月球之间的万有引力
【答案】分析:根据万有引力提供圆周运动的向心力可求中心天体的质量,开普勤第三定律是相对于同一个中心天体的,不同的中心天体该表达式不正确.
解答:解:由题意知,根据万有引力提供向心力有: 可得中心天体的质量M=
可得中心天体的质量M= 所以:
所以:
A、已知月球运动的半径和周期,可以计算出地球的质量M,故A正确;
B、因为地球绕太阳运动,月球绕地球运动,两者中心天体不同,故表达式表达式 =
=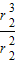 不成立,故B错误;
不成立,故B错误;
C、同A的分析知,可以求出太阳的质量,已知地球和太阳的质量及万有引力常量,可以求出太阳与地球间的万有引力故C正确;
D、因为无法计算出月球的质量,故无法求出地球与月球间的万有引力,故D错误.
故选AC.
点评:万有引力提供向心力是解决本题的关键,牢记据此只能计算出中心天体的质量.
解答:解:由题意知,根据万有引力提供向心力有:
 可得中心天体的质量M=
可得中心天体的质量M= 所以:
所以:A、已知月球运动的半径和周期,可以计算出地球的质量M,故A正确;
B、因为地球绕太阳运动,月球绕地球运动,两者中心天体不同,故表达式表达式
 =
=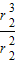 不成立,故B错误;
不成立,故B错误;C、同A的分析知,可以求出太阳的质量,已知地球和太阳的质量及万有引力常量,可以求出太阳与地球间的万有引力故C正确;
D、因为无法计算出月球的质量,故无法求出地球与月球间的万有引力,故D错误.
故选AC.
点评:万有引力提供向心力是解决本题的关键,牢记据此只能计算出中心天体的质量.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
在研究下列哪些问题时,可以把物体看成质点的是( )
| A、比赛时,运动员分析乒乓球的旋转方向时,把乒乓球看作质点 | B、计算在平直马路上行驶的自行车的行驶速度时,把自行车看作质点 | C、研究地球绕太阳作圆周运动时,把地球看作质点 | D、研究自行车车轮轮缘上某点的运动时,把自行车看作质点 |
地球绕太阳作圆周运动的半径为r1、周期为T1;月球绕地球作圆周运动的半径为r2、周期为T2。万有引力常量为G,不计周围其它天体的影响,则根据题中给定条件
| A.能求出地球的质量 | B.表达式 成立 成立 |
| C.能求出太阳与地球之间的万有引力 | D.能求出地球与月球之间的万有引力 |
 成立
成立