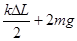题目内容
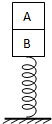 两个物块A、B的质量均为m,叠放在一个竖直的弹簧上,如图所示,弹簧的劲度系数为k,弹簧的质量忽略不计,今用一竖直向下的力F压物块A,弹簧在F的作用下又缩短了△L(弹簧仍在弹性限度内),突然撤去外力F,此时A对B的作用力的大小为( )
两个物块A、B的质量均为m,叠放在一个竖直的弹簧上,如图所示,弹簧的劲度系数为k,弹簧的质量忽略不计,今用一竖直向下的力F压物块A,弹簧在F的作用下又缩短了△L(弹簧仍在弹性限度内),突然撤去外力F,此时A对B的作用力的大小为( )| A、F | ||
| B、F+mg | ||
C、
| ||
D、
|
分析:先根据受力平衡求出原来弹簧的弹力,撤去F后,对AB整体运用牛顿第二定律求出加速度,再隔离A,运用牛顿第二定律求出B对A的作用力,进而根据牛顿第三定律即可求解A对B的作用力的大小.
解答:解:没有F作用在A上时,由平衡条件有:
弹簧的弹力为:F弹=2mg
当F作用在A上时,有:
F+2mg=F弹+k△L
撤去F瞬时,弹簧的弹力不发生变化,根据牛顿第二定律得:
对AB整体,加速度为:a=
=1+
对A,根据牛顿第二定律得:
N-mg=ma
解得:B对A的作用力 N=
+mg
根据牛顿第三定律可知:A对B的作用力为
+mg
故选:C
弹簧的弹力为:F弹=2mg
当F作用在A上时,有:
F+2mg=F弹+k△L
撤去F瞬时,弹簧的弹力不发生变化,根据牛顿第二定律得:
对AB整体,加速度为:a=
| F弹+△ |
| 2m |
| △L |
| 2m |
对A,根据牛顿第二定律得:
N-mg=ma
解得:B对A的作用力 N=
| k△L |
| 2 |
根据牛顿第三定律可知:A对B的作用力为
| k△L |
| 2 |
故选:C
点评:本题主要考查了牛顿第二定律的直接应用,注意整体法和隔离法在题目中的应用.

练习册系列答案
相关题目
 两个物块A、B的质量均为m,叠放在一个竖直的弹簧上,如图所示,弹簧的劲度系数为k,弹簧的质量忽略不计,今用一竖直向下的力F压物块A,弹簧在F的作用下又缩短了△L(弹簧仍在弹性限度内),突然撤去外力F,此时A对B的作用力的大小为( )
两个物块A、B的质量均为m,叠放在一个竖直的弹簧上,如图所示,弹簧的劲度系数为k,弹簧的质量忽略不计,今用一竖直向下的力F压物块A,弹簧在F的作用下又缩短了△L(弹簧仍在弹性限度内),突然撤去外力F,此时A对B的作用力的大小为( ) ,弹簧的质量忽略不计,今用一竖直向下的力F压物块A,弹簧在F的作用下又缩短了
,弹簧的质量忽略不计,今用一竖直向下的力F压物块A,弹簧在F的作用下又缩短了 (弹簧仍在弹性限度内),突然撤去外力F,此时A对B的作用力的大小为
(弹簧仍在弹性限度内),突然撤去外力F,此时A对B的作用力的大小为
 D.
D.