Question

（2005?宿迁模拟）如图所示，MN是一条通过透明体球心的直线．在真空中波长为λ₀=564nm的单色细光束AB平行于MN射向球体，B为入射点．若出射光线CD与MN的交点P到球心O的距离是球半径的

2

倍，且与MN所成的角α=30°，求此单色光在透明球体中的波长和透明体的折射率．

Answer 1

分析：连接OB、BC，在B点光线的入射角、折射角分别标为i、r，作出光路图，根据几何关系求出入射角与折射角，根据折射定律求解折射率，根据波速、波长、频率的关系即可求得此单色光在透明球体中的波长．

解答：解：连接OB、BC，在B点光线的入射角、折射角分别标为i、r，如图所示．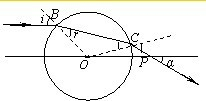
在△OCP中：有

OC

sinα

=

OP

sin∠OCP

解得∠OCP=135°（45°值舍去）
进而可得：∠COP=15°
由折射率定义：在B点有：n=

sini

sinr

在C点有：n=

sin(180°-135°)

sin∠BCO

，
又∠BCO=r
所以，i=45°
又：∠BCO=180°-i-∠COP=120°
  故：r=30° 
因此，透明体的折射率
n=

sini

sinr

=

sin45°

sin30°

=

2

n=

c

v

=

c f

v f

=

λ0

λ

解得：λ=399nm
答：此单色光在透明球体中的波长为399nm，透明体的折射率为

2

．

点评：本题是较为复杂的几何光学问题，其基础是作出光路图，根据几何知识确定入射角与折射角，根据折射定律求解，折射过程中频率不变．