题目内容
 如图所示,两个完全相同的小球A、B用等长的细线悬于O点.线长L.若将A由图示位置静止释放,则B球被碰后第一次速度为零时的高度不可能是( )
如图所示,两个完全相同的小球A、B用等长的细线悬于O点.线长L.若将A由图示位置静止释放,则B球被碰后第一次速度为零时的高度不可能是( )A、
| ||
B、
| ||
C、
| ||
D、
|
分析:A、B两球发生碰撞时有可能是弹性碰撞,有可能是完全非弹性碰撞,利用机械能守恒和动量定理求出这里两个临界点,再进行分析.
解答:解:A球到达最低点时,设其动能为:EkA,
由动能定理得:mgL(1-cos60°)=EkA-0
EkA=
mgL
若:A、B间发生的是弹性碰撞,则B获得动能最大为EkA,上升的最大高度和A释放点相同:
即为:L(1-coθ)=
L
若:A、B间发生的是完全非弹性碰撞(就是两个小球粘在一起):设共同达到的速度为v':
由动量守恒:mv=2mv'
得:v'=
则B获得动能为:
EkA,
由动能定理:
mgh=
×
mgL=
mgL
h=
L
若碰撞介于弹性碰撞和完全非弹性碰撞之间:
上升的高度就介于
L和
L之间.
综上所述:B上升的高度取值范围是:
L≤h≤
L
本题选不可能的,故选:D.
由动能定理得:mgL(1-cos60°)=EkA-0
EkA=
| 1 |
| 2 |
若:A、B间发生的是弹性碰撞,则B获得动能最大为EkA,上升的最大高度和A释放点相同:
即为:L(1-coθ)=
| 1 |
| 2 |
若:A、B间发生的是完全非弹性碰撞(就是两个小球粘在一起):设共同达到的速度为v':
由动量守恒:mv=2mv'
得:v'=
| v |
| 2 |
则B获得动能为:
| 1 |
| 4 |
由动能定理:
mgh=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 8 |
h=
| 1 |
| 8 |
若碰撞介于弹性碰撞和完全非弹性碰撞之间:
上升的高度就介于
| 1 |
| 8 |
| 1 |
| 2 |
综上所述:B上升的高度取值范围是:
| 1 |
| 8 |
| 1 |
| 2 |
本题选不可能的,故选:D.
点评:两物体发生碰撞时,不知道碰撞情况时必须分情况讨论,弹性碰撞或是完全非弹性碰撞.应用动量守恒求解物体碰撞后的速度,再从能量转化的方向去求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
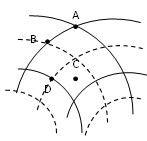
 (2012?金山区一模)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( )
(2012?金山区一模)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( ) (2008?上海模拟)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( )
(2008?上海模拟)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( )