题目内容
由透明介质制成的厚壁容器,其横截面为圆环形,介质的折射率n=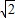 ,内径r=6cm,外径是内径的
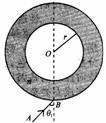
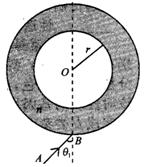
,内径r=6cm,外径是内径的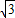 倍,如图所示.一细束光沿AB方向射人容器,入射角θ1=45°,光在空气中的传播速率约取3×108m/s,求这束光从射入到第一次射出透明介质所用的时间是 .
倍,如图所示.一细束光沿AB方向射人容器,入射角θ1=45°,光在空气中的传播速率约取3×108m/s,求这束光从射入到第一次射出透明介质所用的时间是 .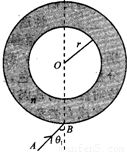
【答案】分析:利用折射定律求折射角,画出光路图,由全反射的条件,判断是否发生全反射,求出光在该介质中的速度,利用运动学知识求时间.
解答: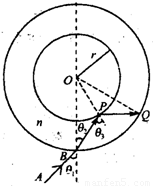 解:从外筒壁入射,设折射角为
解:从外筒壁入射,设折射角为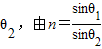 ,
,
可得:θ2=30°
射到内壁界面P处,设入射角为θ3,在△OPB中,根据正弦定理, ,
,
则θ3=60°,
由于临界角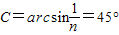 ,
,
在内壁界面处会发生全反射,再次射到外壁界面
处,根据对称性可判断此处的入射角等于θ2,不
会发生全反射,可以从介质中射出.
由数学关系可得,BP=PQ=r=6cm,
在介质中的光速,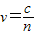
则该光束从射入到第一次射出该介质所用的时间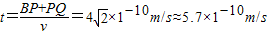
故答案为:5.7×10-10m/s
点评:本题考查了折射、全反射的知识,能正确利用几何知识是解决此类问题的关键.
解答:
 解:从外筒壁入射,设折射角为
解:从外筒壁入射,设折射角为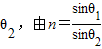 ,
,可得:θ2=30°
射到内壁界面P处,设入射角为θ3,在△OPB中,根据正弦定理,
 ,
,则θ3=60°,
由于临界角
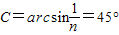 ,
,在内壁界面处会发生全反射,再次射到外壁界面
处,根据对称性可判断此处的入射角等于θ2,不
会发生全反射,可以从介质中射出.
由数学关系可得,BP=PQ=r=6cm,
在介质中的光速,
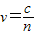
则该光束从射入到第一次射出该介质所用的时间
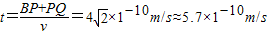
故答案为:5.7×10-10m/s
点评:本题考查了折射、全反射的知识,能正确利用几何知识是解决此类问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 由透明介质制成的厚壁容器,其横截面为圆环形,介质的折射率n=
由透明介质制成的厚壁容器,其横截面为圆环形,介质的折射率n= (1)一列简谐波沿波的传播方向先后有相距6m的A、B两点,A靠近波源,且A、B间距离小于该波3倍波长.当A点位移达到正向最大时,B点的位移恰好为零,且向正向运动.经0.5s(小于该波的4倍周期)后,A点位移恰好为零,且沿正向运动,而B点的位移恰好达到负的最大.则这列波的波速:( )
(1)一列简谐波沿波的传播方向先后有相距6m的A、B两点,A靠近波源,且A、B间距离小于该波3倍波长.当A点位移达到正向最大时,B点的位移恰好为零,且向正向运动.经0.5s(小于该波的4倍周期)后,A点位移恰好为零,且沿正向运动,而B点的位移恰好达到负的最大.则这列波的波速:( )