题目内容
如图甲所示,两平行金属板接有如图乙所示随时间t变化的电压U,两板间电场可看作均匀的,且两板外无电场,板长L=0.2 m,板间距离d=0.2 m.在金属板右侧有一边界为MN的区域足够大的匀强磁场,MN与两板中线OO′垂直,磁感应强度B=5×10-3T,方向垂直纸面向里.现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子速度v0=105 m/s,比荷q/m=108 C/kg,重力忽略不计,在每个粒子通过电场区域的极短时间内,电场可视作是恒定不变的.

(1)试求带电粒子射出电场时的最大速度;
(2)证明:在任意时刻从电场射出的带电粒子,进入磁场时在MN上的入射点和在MN上出射点的距离为定值,写出该距离的表达式;
(3)从电场射出的带电粒子,进入磁场运动一段时间后又射出磁场,求粒子在磁场中运动的最长时间和最短时间.
(1)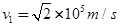 (2)
(2)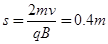 (3)
(3)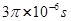 ,
,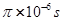
【解析】
试题分析:(1)设两板间电压为U1时,带电粒子刚好从极板边缘射出电场,则有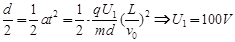 (2分)
(2分)
粒子刚好从极板边缘射出电场时,速度最大,设最大速度为v1,则有: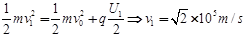 (2分)
(2分)
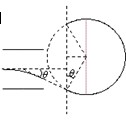
(2)设粒子进入磁场时速度方向与OO'的夹角为θ,速度大小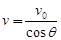 ,则
,则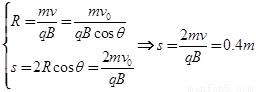 (4分)
(4分)
s与θ无关,即射出电场的任何一个带电粒子进入磁场的入射点与出射点间距离恒为定值.
(3)粒子飞出电场进入磁场,在磁场中按逆时针方向做匀速圆周运动.粒子飞出电场时的速度方向与OO'的最大夹角为α,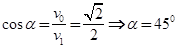 .
.
当粒子从下板边缘飞出电场再进入磁场时,在磁场中运动时间最长:
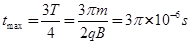 ; (2分)
; (2分)
当粒子从上板边缘飞出电场再进入磁场时,在磁场中运动时间最短:
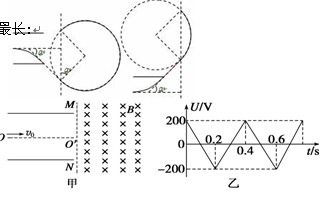
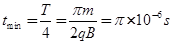 . (2分)
. (2分)
考点:考查了带电粒子在磁场中的偏转问题
点评:带电粒子以一定的速度进入匀强磁场,在洛伦兹力的作用下做匀速圆周运动.粒子在磁场中运动的周期仅与粒子的比荷有关,而运动的时间与偏转角有关.当入射速度越大时,运动轨道的半径越大,而向心加速度由速度与半径来确定

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案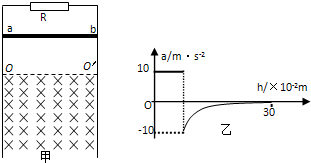 (2011?徐州一模)如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:
(2011?徐州一模)如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:

 如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:
如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求: =1x108C/kg、初速度v0=2x 105m/s的带正电粒子.忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极 板间的电压变化.sin30=0.5,sin37=0.6,sin45=
=1x108C/kg、初速度v0=2x 105m/s的带正电粒子.忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极 板间的电压变化.sin30=0.5,sin37=0.6,sin45= .
.