题目内容
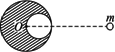
有一质量为M、半径为R、密度均匀的球体,在距离球心O为2R的地方有一质量为m的质点,现在从M中挖去一半径为![]() 的球体,如图所示.求剩下部分对m的万有引力F为多大?
的球体,如图所示.求剩下部分对m的万有引力F为多大?
答案:
解析:
解析:
|
解析:一个质量均匀分布的球体与球外的一个质点间的万有引力可以用公式F=G 设被挖小球的质量为 由题意知 F1=G F2=G 所以F=F1-F2= 方法归纳 仔细观察球体挖去部分及完整球体的形状特点,可知,完整部分与质点m以及挖去部分与质点m间万有引力均可用公式计算,由此联想到利用等效割补的方式先将剩余部分还原为完整体,计算出万有引力,然后计算出割去部分与质点m间的万有引力,两者之差即为所求.通过“割补法”的运用,可以感受利用直觉思维寻求解题思路的简捷性. |

练习册系列答案
相关题目
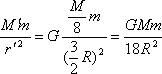

 的球体,如图所示,求剩下部分对m的万有引力F为多大?
的球体,如图所示,求剩下部分对m的万有引力F为多大?

