题目内容
如图所示，现有一个小物块，质量为m=80g，带上正电荷q =2
10－4C。与水平的轨道之间的滑动摩擦系数m= 0.2，在一个水平向左的匀强电场中，E = 4103V/m，在水平轨道的末端N处，连接一个光滑的的半圆形轨道，半径为R=40cm，取g = 10m/s2，求：
（1）若小物块恰能运动到轨道的最高点L，那么小物块应从距N点多远处的A点释放？
（2）如果小物块在上小题中的位置A释放，当它运动到P点（轨道中点）时轨道对它的支持力等于多少？
（3）小物块在位置A释放，当运动到N点时，突然撤去电场，同时加一匀强磁场，磁感应强度
，方向垂直纸面向里，问能否运动到L点？（回答：“能”或“不能”即可）如果小物块最后能落回到水平面MN上，则刚到达MN时小物块的速度大小为多少？
解析（1）物块能通过轨道最高点L的条件是
…………（2分） vL=2m/s ………… （1分）
A到L过程： 
…………（2分）
解得 s=1.25m ………… （1分）
（2）物块由P到L过程：
………… （2分）
VP=2
m/s ………… （1分）
P点：
………… （2分）
FN=4.8N …… …………（1分）
（3）能 ………… ………… （3分）
小物块落回到MN水平面时，速度的大小vt等于第一次经过N点时的速度大小。
由动能定理:
………… （2分）（或考虑物块N由L到过程,解答也可）
vt=
=
………… （1分）
练习册系列答案
相关题目
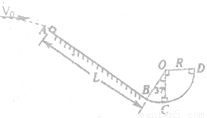
如图所示，粗糙的斜面AB下端与光滑的圆弧轨道BCD相切于B，整个装置竖直放置，C是最低点，圆心角∠BOC=37°，圆弧轨道半径R=0.5m，斜面长L=2m，整个轨道除AB段以外都是光滑的，如图所示．现有一个质量m=0.1kg的小物块以初速度vo=4m/s，从某一高处水平抛出，到A点时速度方向恰沿AB方向，并沿倾斜轨道滑下．已知物块与倾斜轨道的动摩擦因数μ=0.5（g取10m/s2，sin37°=0.60，cos37°=0.08）．
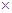10－4C。与水平的轨道之间的滑动摩擦系数m= 0.2，在一个水平向左的匀强电场中，E
= 4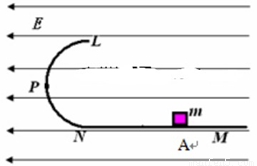
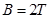，方向垂直纸面向里，问能否运动到L点？（回答：“能”或“不能”即可）如果小物块最后能落回到水平面MN上，则刚到达MN时小物块的速度大小为多少？
