题目内容
16．
如图所示为水平导轨，A、B为弹性竖直挡板，相距L=4m．小球自A板处开始，以V0=4m/s的速度沿导轨向B运动．它与A、B挡板碰撞后均以与碰前大小相等的速率反弹回来，且在导轨上做减速运动的加速度大小不变．为使小球停在AB的中点，这个加速度的大小可能为（ ）
| A． | 0.8m/s2 | B． | $\frac{4}{3}$m/s2 | C． | 1.5m/s2 | D． | 4m/s2 |
分析 已知物体在碰到A或B以后，均以与碰前等大的速度反弹回来，可将该运动看成在一条直线上做方向不变的匀减速直线运动，根据物体停在AB中点，得出运动的路程s=nL+$\frac{L}{2}$，然后根据匀变速直线运动的速度位移公式vt2-v02=2as求出加速度的大小．
解答 解：物体停在AB的中点，可知物体的路程s=nL+$\frac{L}{2}$，由vt2-v02=2as得，a=$\frac{{v}^{2}}{2（nL+\frac{L}{2}）}$，n=0，1，2，…．
代入数据解得a=$\frac{4}{2n+1}$m/s2．n=0，1，2，…，当n=0时，a=4m/s2，当n=1时，a=$\frac{4}{3}$m/s2，当n=2时，a=0.8m/s2，故ABD正确，C错误．
故选：ABD
点评 解决本题的关键将该运动看成在一条直线上做方向不变的匀减速直线运动，以及掌握匀变速直线运动的速度位移公式vt2-v02=2as．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．
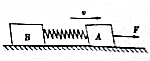如图所示，A，B两个物体通过一轻弹簧相连，已知mA=1kg，mB=2kg，现对A施加一大小为3N的水平恒力F，使它们一起沿粗糙的水平地面向右做匀速运动，某时刻突然撤去力F．此时A，B两物体的加速度分别aA，aB，则（ ）
如图所示，A，B两个物体通过一轻弹簧相连，已知mA=1kg，mB=2kg，现对A施加一大小为3N的水平恒力F，使它们一起沿粗糙的水平地面向右做匀速运动，某时刻突然撤去力F．此时A，B两物体的加速度分别aA，aB，则（ ）| A． | aA=aB=0 | |
| B． | aA=3m/s2，方向水平向左，aB=0 | |
| C． | aA=aB=1m/s2，方向水平向左 | |
| D． | aA=3m/s2，方向水平向右，aB=1.5m/s2，方向水平向左 |
电阻可忽略的光滑平行金属导轨长S=1.4m，两导轨间距L=0.75m，导轨倾角为θ=30°，导轨上端ab接一阻值R=1.5Ω的电阻，磁感应强度B=0.8T的匀强磁场垂直轨道平面向上．阻值r=1.5Ω，质量m=0.2kg的金属棒与轨道垂直且接触良好，从轨道上端ab处由静止开始下滑至底端，在此过程中电阻R产生的焦耳热Q=0.3J． g取10m/s2，求：
11．一质点做直线运动，t=0时刻，v＞0，a＞0，此后a逐渐减小至零的过程中（ ）
| A． | 速度的变化越来越快 | B． | 速度逐步减小 | ||
| C． | 位移继续增大 | D． | 位移、速度始终为正值 |
1．下列带下划线的物体能看做质点的是（ ）
| A． | 沿着斜面下滑的木块 | B． | 研究刘翔跨栏中的动作 | ||
| C． | 原子核很小，一定能看成质点 | D． | 研究地球的各区域气候变化 |
受动画片《四驱兄弟》的影响，越来越多的小朋友喜欢上了玩具赛车．某玩具赛车充电电池的输出功率P随电流I变化的图象如图所示．
6．
取一只扁玻璃瓶，里面盛满水，用穿有透明细管的橡皮塞封口，使水面位于细管中（如图）．用手捏玻璃瓶，可以看到透明细管中的水面变化，这一实验的目的是（ ）
取一只扁玻璃瓶，里面盛满水，用穿有透明细管的橡皮塞封口，使水面位于细管中（如图）．用手捏玻璃瓶，可以看到透明细管中的水面变化，这一实验的目的是（ ）| A． | 说明玻璃瓶中的水可以发生形变 | B． | 说明玻璃瓶可以发生形变 | ||
| C． | 验证弹力的大小跟形变量成正比 | D． | 验证水热胀冷缩 |