题目内容
如图,一质量为M的物块静止在光滑水平桌面的边缘,桌面离水平面的高度为h,一质量为m的子弹以水平速度v射入物块后,以水平速度v/2射出,重力加速度为g.已知M=3m,求:(1)此过程中系统损失的机械能;
(2)此后物块落地点离桌面边缘的水平距离.

【答案】分析:(1)子弹射击物块,子弹和物块的总动量守恒,由动量守恒定律求出子弹穿出木块时木块的速度大小.系统损失的机械能等于射入前子弹的动能与射出后物块与子弹总动能之差.
(2)子弹射出物块后,物块做平抛运动,由高度求出时间,再求出水平距离.
解答:解:(1)设子弹穿过物块后物块的速度为V,由动量守恒得
mv=m +Mv…①?
+Mv…①?
解得v= v
v
系统的机械能损失为
△E= mv2-
mv2- m(
m( )2-
)2- Mv2…③
Mv2…③
解得△E= m
m
(2)设物体下落到地面所需时间为t,落地点距桌面边缘的水平距离为s,则
h= gt2
gt2
s=vt
解得:s=

答:(1)此过程中系统损失的机械能是△E= m
m ;
;
(2)此后物块落地点离桌面边缘的水平距离是
 .
.
点评:本题采用程序法按时间顺序进行分析处理,是动量守恒定律与平抛运动简单的综合,比较容易.
(2)子弹射出物块后,物块做平抛运动,由高度求出时间,再求出水平距离.
解答:解:(1)设子弹穿过物块后物块的速度为V,由动量守恒得
mv=m
 +Mv…①?
+Mv…①?解得v=
 v
v系统的机械能损失为
△E=
 mv2-
mv2- m(
m( )2-
)2- Mv2…③
Mv2…③解得△E=
 m
m
(2)设物体下落到地面所需时间为t,落地点距桌面边缘的水平距离为s,则
h=
 gt2
gt2s=vt
解得:s=


答:(1)此过程中系统损失的机械能是△E=
 m
m ;
;(2)此后物块落地点离桌面边缘的水平距离是

 .
.点评:本题采用程序法按时间顺序进行分析处理,是动量守恒定律与平抛运动简单的综合,比较容易.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 如图,一质量为M的物块被两竖直板用力F夹住,物与板间的摩擦系数为μ,要使物块匀速向上运动而两竖直板不动,向上拉物块的力最小为
如图,一质量为M的物块被两竖直板用力F夹住,物与板间的摩擦系数为μ,要使物块匀速向上运动而两竖直板不动,向上拉物块的力最小为 如图,一质量为M的物块静止在桌面边缘,桌面离水平地面高度为h,质量为m的子弹以水平速度v0射入物块后,以水平速度
如图,一质量为M的物块静止在桌面边缘,桌面离水平地面高度为h,质量为m的子弹以水平速度v0射入物块后,以水平速度 如图:一质量为M的物块被两竖直板用力F夹住,物与板间的摩擦系数为μ,要使物块匀速向上运动而两竖直板不动,向上拉物块的力为
如图:一质量为M的物块被两竖直板用力F夹住,物与板间的摩擦系数为μ,要使物块匀速向上运动而两竖直板不动,向上拉物块的力为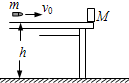 如图,一质量为M的物块静止在桌面边缘,桌面离水平地面的高度为h.一质量为m的子弹以水平速度v0射入物块后,以水平速度v0/2 射出.重力加速度为g.求:
如图,一质量为M的物块静止在桌面边缘,桌面离水平地面的高度为h.一质量为m的子弹以水平速度v0射入物块后,以水平速度v0/2 射出.重力加速度为g.求: