题目内容
静止的放射性原子核
X发生α衰变时,设放出的能量都转变成了α粒子和新核Y的动能,若测得α粒子的动能为E,求:
(1)新核Y的动能
(2)此衰变过程中的质量亏损.
m z |
(1)新核Y的动能
(2)此衰变过程中的质量亏损.
分析:(1)根据动量守恒定律得出α粒子和新核Y动量的关系,结合动量和动能的关系求出新核的动能.
(2)结合释放的能量,通过爱因斯坦质能方程求出衰变过程中的质量亏损.
(2)结合释放的能量,通过爱因斯坦质能方程求出衰变过程中的质量亏损.
解答:解:(1)根据动量守恒定律得:O=Pα-PY
因为动能Ek=
,可知新核的动能与α粒子的动能之比等于质量之反比,即
=
所以新核的动能EY=
.
(2)衰变过程中释放的能量△E=E+EY
根据△E=△mc2
解得△m=
.
答:(1)新核Y的动能为
.
(2)衰变中的质量亏损为
因为动能Ek=
| P2 |
| 2m |
| EY |
| E |
| 4 |
| m-4 |
所以新核的动能EY=
| 4E |
| m-4 |
(2)衰变过程中释放的能量△E=E+EY
根据△E=△mc2
解得△m=
| mE |
| (m-4)c2 |
答:(1)新核Y的动能为
| 4E |
| m-4 |
(2)衰变中的质量亏损为
| mE |
| (m-4)c2 |
点评:解决本题的关键知道在衰变的过程中动量守恒,α粒子的动量大小和新核的动量大小相等.以及掌握爱因斯坦质能方程,并能灵活运用.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
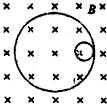 一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了衰变而形成了如图所示的两个圆形径迹,两圆半径之比为1:16,则以下说法正确的是( )
一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了衰变而形成了如图所示的两个圆形径迹,两圆半径之比为1:16,则以下说法正确的是( )| A、该原子核发生了α衰变 | B、反冲核沿小圆做逆时针方向运动 | C、原静止的原子核的原子序数为17 | D、沿大圆和沿小圆运动的粒子的周期相同 |
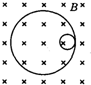 一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了衰变而形成了如图所示的两个圆形径迹,两圆半径之比为1:16( )
一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了衰变而形成了如图所示的两个圆形径迹,两圆半径之比为1:16( ) 一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了某种衰变而形成了如图所示的两个圆形径迹,两圆半径之比为1:16,有( )
一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了某种衰变而形成了如图所示的两个圆形径迹,两圆半径之比为1:16,有( ) (2006?武汉模拟)一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生衰变而形成如图所示的两个圆形径迹,两圆半径之比为 1:16,则( )
(2006?武汉模拟)一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生衰变而形成如图所示的两个圆形径迹,两圆半径之比为 1:16,则( )