Question

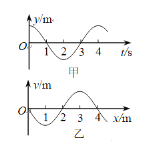
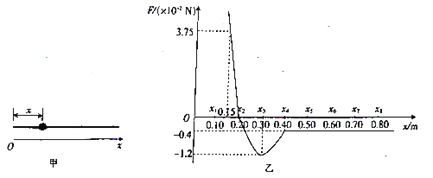
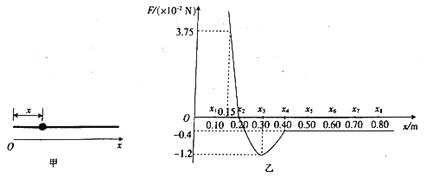
【题目】如图甲所示，质量m=0.02 kg的有孔小球套在水平光滑的细杆上，以杆的左端为原点，沿杆向右为工轴正方向建立坐标轴Ox。小球受到沿杆的水平外力F随小球到细杆左端的距离x的关系如图乙所示(外力F为正表示其方向水平向右)，在0≤x≤0.20m和x≥0.40m范围内的图线为直线，其他范围内为曲线。若小球在x2=0.20m处的速度大小v=0.4m/s、方向水平向右，则其向右最远可以运动到x4=0.40m处。

（1）求小球从工运动到工的过程中的最大加速度；

（2）若将小球x6=0.60m处由静止释放，求小球释放后向左运动的最大距离。

Answer 1

【答案】（1）（2）0.48m

【解析】（1）小球从运动到的过程中，经过对处时F最大，其最大值为：

由牛顿第二定律有： ，解得：

（2）设小球从运动到的过程中克服F所做的功为，由动能定理有：

解得： J

设小球从运动到的过程中F所做的功为则有，

其中

解得：

由对称性可知，小球从运动到的过程中F所做的功为： J

经分析可知，小球到达后继续向左运动，设小球向左运动的最远处到处的距离为，

且小球在处时F的大小为，则有：

小球从向左运动到最远处的过程中，由动能定理有：

解得：

故：