题目内容
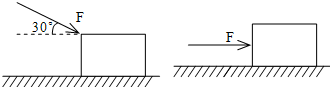 如图所示,一个人用与水平方向成θ=30°角斜向 的推力F推一个重为G=200N的箱子匀速前进,箱子与地面间的动摩擦因数为μ=0.40.求:
如图所示,一个人用与水平方向成θ=30°角斜向 的推力F推一个重为G=200N的箱子匀速前进,箱子与地面间的动摩擦因数为μ=0.40.求:(1)推力F的大小;
(2)若人不改变推力F的大小,只把力的方向变为水平,去推这个静止的箱子,且当作用的时间t=3s后撤去推力,则撤去推力后箱子还能运动多长时间?
分析:(1)对箱子受力分析,受重力、支持力、推力和滑动摩擦力,根据平衡条件列式求解;
(2)分加速和减速两个过程,先求解加速度,然后根据运动学公式列式求解.
(2)分加速和减速两个过程,先求解加速度,然后根据运动学公式列式求解.
解答:解:(1)对箱子受力分析,受重力、支持力、推力和滑动摩擦力,根据平衡条件,有:
水平方向:Fcos30°-f=0;
竖直方向:Fsin30°+G=N
其中:f=μN
联立解得:
F=
=
=120.3N
(2)加速解得加速度:a=
=
=2m/s2
加速过程的末速度为:v=a1t=6 m/s
减速过程加速度大小为μg;
根据速度时间关系公式,有:t=
=
=1.5s
答:(1)推力F的大小为120.3N;
(2)撤去推力后箱子还能运动1.5s的时间.
水平方向:Fcos30°-f=0;
竖直方向:Fsin30°+G=N
其中:f=μN
联立解得:
F=
| μG |
| cos30°-μsin30° |
| 0.4×200 | ||||||
|
(2)加速解得加速度:a=
| F-μG |
| m |
| 120.3=0.4×200 |
| 20 |
加速过程的末速度为:v=a1t=6 m/s
减速过程加速度大小为μg;
根据速度时间关系公式,有:t=
| v |
| μg |
| 6 |
| 0.4×10 |
答:(1)推力F的大小为120.3N;
(2)撤去推力后箱子还能运动1.5s的时间.
点评:本题关键是受力分析后根据平衡条件求解推力;然后受力分析后根据牛顿第二定律确定加速度大小,最后根据运动学公式列式求解.

练习册系列答案
相关题目
 如图所示,一个人用与水平方向37°的力F=20N推一个静止在水平面上质量为2kg的物体,物体和地面间的动摩擦因数为0.1.(sin37=0.6,cos37=0.8)求:
如图所示,一个人用与水平方向37°的力F=20N推一个静止在水平面上质量为2kg的物体,物体和地面间的动摩擦因数为0.1.(sin37=0.6,cos37=0.8)求: 如图所示,一个人用与水平方向成θ=30°角的斜向下的推力F推一个重G=200N的箱子匀速前进,箱子与地面间的动摩擦因数为μ=0.4,g取10m/s2.
如图所示,一个人用与水平方向成θ=30°角的斜向下的推力F推一个重G=200N的箱子匀速前进,箱子与地面间的动摩擦因数为μ=0.4,g取10m/s2. 如图所示,一个人用与水平方向成37°的力F=20N推一个静止在水平面上质量为2kg的物体,物体仍然保持静止状态.(cos37°=0.8,sin37°=0.6,g取10m/s2)求:
如图所示,一个人用与水平方向成37°的力F=20N推一个静止在水平面上质量为2kg的物体,物体仍然保持静止状态.(cos37°=0.8,sin37°=0.6,g取10m/s2)求: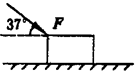 如图所示,一个人用与水平方向成37°的力F=20N推一个静止在水平面上质量为2kg的物体,物体和地面间的动摩擦因数为0.1.(cos37°=0.8,sin37°=0.6)求
如图所示,一个人用与水平方向成37°的力F=20N推一个静止在水平面上质量为2kg的物体,物体和地面间的动摩擦因数为0.1.(cos37°=0.8,sin37°=0.6)求