题目内容
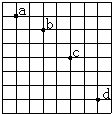
【题目】如图所示，长木板的质量为M=3m，长度为L，放在光滑水平面上距墙壁足够远处，在木板A的左端放一个可视为质点的物体B，质量为m，A与B的动摩擦因数为μ，给B一个初速度
，已知木板与墙壁碰撞时间极短，且碰后以原速率弹回．当长木板与墙壁碰撞时，在墙壁的左边所有空间加一个竖直向上的匀强电场(物体B带正电，且电量为q，并保持恒定)，求：
（1）木板与墙壁相碰时，物块与墙壁的距离；
（2）如果木板与墙壁碰后的运动过程中物体恰好不能离开木板A，试求电场强度E.
【答案】（1）
（2）
【解析】试题分析：由牛顿第二定律求出加速度，由匀变速直线运动的运动学公式求出物块与墙壁间的距离．由匀变速直线运动的运动规律求出加速度，然后应用牛顿第二定律求出电场强度．
（1）由牛顿第二定律得：对物块：
，对木板：
，
由匀变速直线运动的速度公式得：
，
则物块位移
，木板位移：
，
，因此物体与墙壁的距离为
（2）速度
，
则物块：
，木板：
，
,得
，
由牛顿第二定律得：
，
，得
.
练习册系列答案
相关题目
