题目内容
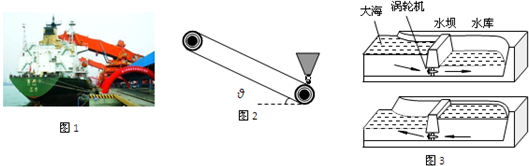
 如图所示,传送带与水平地面间的倾角为θ=37°,从A端到B端长度为s=16m,传送带在电机带动下始终以v=10m/s的速度逆时针运动,在传送带上A端由静止释放一个质量为m=0.5kg的可视为制质点的小物体,它与传送带之间的动摩擦因数为μ=0.5,假设最大静摩擦力与滑动摩擦力大小相同,g取10m/s2,sin37°=0.6,求:
如图所示,传送带与水平地面间的倾角为θ=37°,从A端到B端长度为s=16m,传送带在电机带动下始终以v=10m/s的速度逆时针运动,在传送带上A端由静止释放一个质量为m=0.5kg的可视为制质点的小物体,它与传送带之间的动摩擦因数为μ=0.5,假设最大静摩擦力与滑动摩擦力大小相同,g取10m/s2,sin37°=0.6,求:(1)小物体从A到B所用的时间.
(2)在小物体从A到B的过程中,电动机对传送带做的总功.
分析:(1)物块轻轻放到传送带上,受重力、支持力和沿斜面向下的滑动摩擦力,做匀加速直线运动.当速度达到10m/s,由于物体不能跟传送带保持相对静止,受重力、支持力和沿斜面向上的滑动摩擦力,做匀加速直线运动,根据牛顿第二定律求出两段匀加速直线运动的加速度,根据运动学公式求出运动的总时间.
(2)在小物体从A到B的过程中,对物体和皮带系统运用动能定理列式求解即可.
(2)在小物体从A到B的过程中,对物体和皮带系统运用动能定理列式求解即可.
解答:解:(1)煤块放上传送带后的加速度:
a1=
=gsin37°+μgcos37°=10m/s2
因为mgsin37°>μmgcos37°
所以煤炭的速度与传送带速度相等后,做匀加速直线运动,加速度:
a2=
=gsin37°-μgcos37°=2m/s2
速度相等前匀加速运动的时间:
t1=
=
=1s
位移:
x1=
a1t12=
×10×1m=5m
速度相等后匀加速运动的位移x2=s-x1=11m
x2=vt2+
a2t22,代入数据解得:t2=1s
t=t1+t2=2s
故物体在传送带上运动的总时间为2s.
(2)速度相等前,物块相对于传送带向后滑.
x1′=vt1=10m
则△x1=x1′-x1=5m
速度相等后,物块相对于传送带向前滑.
x2′=vt2=10m
△x2=x2-x2′=1m
物体的末速度为:vt=v+a2t2=10+2×1=12m/s;
设电动机对传送带做的总功为W1,对物体和皮带系统运用动能定理,有:
W1+mgSsin37°-μmgcos37°(△x1+△x2)=
mvt2-0
解得:
W1=
mvt2-mgSsin37°+μmgcos37°(△x1+△x2)=
×0.5×122-0.5×10×16×0.6+0.5×0.5×10×0.8×(5+1)=0;
答:(1)小物体从A到B所用的时间为2s.
(2)在小物体从A到B的过程中,电动机对传送带做的总功为零.
a1=
| mgsin37°+μmgcos37° |
| m |
因为mgsin37°>μmgcos37°
所以煤炭的速度与传送带速度相等后,做匀加速直线运动,加速度:
a2=
| mgsin37°-μmgcos37° |
| m |
速度相等前匀加速运动的时间:
t1=
| v |
| a1 |
| 10 |
| 10 |
位移:
x1=
| 1 |
| 2 |
| 1 |
| 2 |
速度相等后匀加速运动的位移x2=s-x1=11m
x2=vt2+
| 1 |
| 2 |
t=t1+t2=2s
故物体在传送带上运动的总时间为2s.
(2)速度相等前,物块相对于传送带向后滑.
x1′=vt1=10m
则△x1=x1′-x1=5m
速度相等后,物块相对于传送带向前滑.
x2′=vt2=10m
△x2=x2-x2′=1m
物体的末速度为:vt=v+a2t2=10+2×1=12m/s;
设电动机对传送带做的总功为W1,对物体和皮带系统运用动能定理,有:
W1+mgSsin37°-μmgcos37°(△x1+△x2)=
| 1 |
| 2 |
解得:
W1=
| 1 |
| 2 |
| 1 |
| 2 |
答:(1)小物体从A到B所用的时间为2s.
(2)在小物体从A到B的过程中,电动机对传送带做的总功为零.
点评:解决本题第一问的关键理清物体的运动情况,根据受力去求运动,加速度是联系前后的桥梁.第二问关键对系统运用动能定理列式求解.

练习册系列答案
相关题目
 如图所示为一皮带传送装置,皮带保持匀速率运动,货物由静止放到传送带上,被传送带向下传送,其运动的v-t图象如图乙所示.
如图所示为一皮带传送装置,皮带保持匀速率运动,货物由静止放到传送带上,被传送带向下传送,其运动的v-t图象如图乙所示.