题目内容
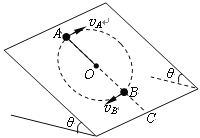
【题目】如图所示，在倾角为θ的光滑斜面上，有一长为l的细线，细线的一端固定在O点，另一端拴一质量为m的小球，现使小球恰好能在斜面上做完整的圆周运动，最高点为A，最低点为B，B到底边C点的距离为S，求：
(1）小球通过最高点A时的速度
．
(2）小球通过最低点B时，细线对小球的拉力．
（3）若小球在最低点B时绳刚好断裂，求小球滑落到底边时到C点的距离。
【答案】(1) 
；(2)6mgsin
； （3）
【解析】(1)小球恰能在斜面上做完整的圆周运动，通过A点细线拉力为零，由牛顿第二定律： 
；解得： 
；
(2)小球从A点运动到B点，根据机械能守恒定律有：
解得： 
小球在B点时由牛顿第二定律： 
解得： 
（3）因
沿着斜面方向加速度为
； 
平行于斜面方向
练习册系列答案
相关题目
