题目内容
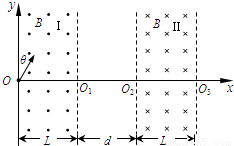
扭摆器是同步辐射装置中的插入件,能使粒子的运动轨迹发生扭摆,其简化模型如图所示:Ⅰ、Ⅱ两处宽度均为L的条形匀强磁场区边界竖直,Ⅰ区域磁场垂直纸面向外,Ⅱ区域磁场垂直纸面向里,磁感应强度大小均为B,两磁场区的间距可以调节.以Ⅰ区域左边界上的O点为坐标原点建立坐标系,y轴与左边界重合,x轴与磁场边界的交点分别为O1、O2和O3.一质量为m、电荷量为q的带正电的粒子,平行纸面从O点与y轴的夹角θ=30°射入Ⅰ区域,粒子重力不计.(1)若粒子恰好从O1射出Ⅰ区域,粒子的速度应为多大?
(2)若粒子从Ⅰ区域右边界射出时速度与x轴的夹角为30°,调节两磁场区的间距,粒子恰好从O3射出Ⅱ区域,则粒子从O射入到从O3射出共经历了多长时间?
【答案】分析:(1)根据几何关系得出粒子在磁场中运动的半径大小,结合带电粒子在磁场中运动半径公式求出粒子速度的大小.
(2)作出带电粒子在磁场中运动的轨迹,根据几何关系得出粒子在磁场中运动的圆心角,以及在无磁场区运动的位移和轨道半径的关系,根据对称性,得出带电粒子在磁场中运动的时间和无磁场区运动的时间,从而求出总时间.
解答: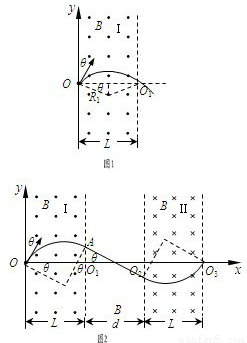 解:(1)粒子从O1射出Ⅰ区域,轨迹如图1.
解:(1)粒子从O1射出Ⅰ区域,轨迹如图1.
由几何关系2R1cosθ=L
粒子在磁场中的运动半径公式R1=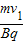 .
.
综合上式可得v1=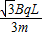 .
.
(2)粒子的运动轨迹如图2所示.
设粒子的运动速度为v2,半径R2=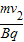
粒子在磁场中的运动周期T=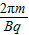
由几何关系可得,粒子在Ⅰ区运动的圆心角为90°
即tⅠ=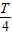
A O1=R2cosθ-R2sinθ
由于粒子Ⅰ、Ⅱ两区域的运动半径相同,要使粒子从O3射出Ⅱ区域,则粒子在Ⅱ区中运动时间与Ⅰ区相同,且粒子必须经过O1 O2的中点B
则tⅡ=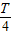
在ⅠⅡ间隔区域运动的时间t2=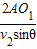 =
=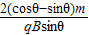 .
.
综上所述,粒子从O射入到O3射出共经历的时间为
t=tⅠ+t2+tⅡ=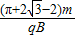 .
.
答:(1)粒子的速度应为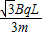 .
.
(2)粒子从O射入到从O3射出共经历时间为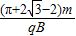 .
.
点评:本题考查带电粒子在磁场中的运动,掌握粒子在磁场中运动的轨道半径公式和周期公式.本题对数学几何能力的要求较高,以及注意粒子恰好从O3射出Ⅱ区域,在两个磁场运动的轨迹是对称的.
(2)作出带电粒子在磁场中运动的轨迹,根据几何关系得出粒子在磁场中运动的圆心角,以及在无磁场区运动的位移和轨道半径的关系,根据对称性,得出带电粒子在磁场中运动的时间和无磁场区运动的时间,从而求出总时间.
解答:
 解:(1)粒子从O1射出Ⅰ区域,轨迹如图1.
解:(1)粒子从O1射出Ⅰ区域,轨迹如图1.由几何关系2R1cosθ=L
粒子在磁场中的运动半径公式R1=
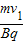 .
.综合上式可得v1=
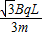 .
.(2)粒子的运动轨迹如图2所示.
设粒子的运动速度为v2,半径R2=
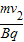
粒子在磁场中的运动周期T=
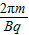
由几何关系可得,粒子在Ⅰ区运动的圆心角为90°
即tⅠ=
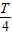
A O1=R2cosθ-R2sinθ
由于粒子Ⅰ、Ⅱ两区域的运动半径相同,要使粒子从O3射出Ⅱ区域,则粒子在Ⅱ区中运动时间与Ⅰ区相同,且粒子必须经过O1 O2的中点B
则tⅡ=
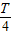
在ⅠⅡ间隔区域运动的时间t2=
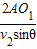 =
=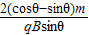 .
.综上所述,粒子从O射入到O3射出共经历的时间为
t=tⅠ+t2+tⅡ=
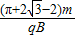 .
.答:(1)粒子的速度应为
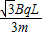 .
.(2)粒子从O射入到从O3射出共经历时间为
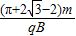 .
.点评:本题考查带电粒子在磁场中的运动,掌握粒子在磁场中运动的轨道半径公式和周期公式.本题对数学几何能力的要求较高,以及注意粒子恰好从O3射出Ⅱ区域,在两个磁场运动的轨迹是对称的.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案
相关题目
 扭摆器是同步辐射装置中的插入件,能使粒子的运动轨迹发生扭摆,其简化模型如图所示:Ⅰ、Ⅱ两处宽度均为L的条形匀强磁场区边界竖直,Ⅰ区域磁场垂直纸面向外,Ⅱ区域磁场垂直纸面向里,磁感应强度大小均为B,两磁场区的间距可以调节.以Ⅰ区域左边界上的O点为坐标原点建立坐标系,y轴与左边界重合,x轴与磁场边界的交点分别为O1、O2和O3.一质量为m、电荷量为q的带正电的粒子,平行纸面从O点与y轴的夹角θ=30°射入Ⅰ区域,粒子重力不计.
扭摆器是同步辐射装置中的插入件,能使粒子的运动轨迹发生扭摆,其简化模型如图所示:Ⅰ、Ⅱ两处宽度均为L的条形匀强磁场区边界竖直,Ⅰ区域磁场垂直纸面向外,Ⅱ区域磁场垂直纸面向里,磁感应强度大小均为B,两磁场区的间距可以调节.以Ⅰ区域左边界上的O点为坐标原点建立坐标系,y轴与左边界重合,x轴与磁场边界的交点分别为O1、O2和O3.一质量为m、电荷量为q的带正电的粒子,平行纸面从O点与y轴的夹角θ=30°射入Ⅰ区域,粒子重力不计.