题目内容
某研究性学习小组用如图所示的装置来选择密度相同、大小不同的球状纳米粒子.密度相同的粒子在电离室中被电离后带正电,电量与其表面积成正比.电离后粒子缓慢通过小孔O1进入极板间电压为U的水平加速电场区域I,再通过小孔O2射入相互正交的恒定匀强电场和匀强磁场区域II,其中磁场的磁感应强度大小为B,方向垂直纸面向外.收集室的小孔O3与O1、O2在同一条水平线上.实验发现:半径为r的粒子,其质量为m、电量为q,刚好能沿O1O3直线射入收集室.不计纳米粒子重力和粒子之间的相互作用力.(球形体积和球形面积公式分别为V球= πr3,S球=4πr2).求:
πr3,S球=4πr2).求:
(1)图中区域II的电场强度E;
(2)半径为r的粒子通过O2时的速率v;
(3)试讨论半径r≠r的粒子进入区域II后将向哪个极板偏转.
【答案】分析:(1)带电粒子在电场中被加速,当进入区域II内做匀速直线运动,因而根据动能定理可求出被加速的速度大小,再由洛伦兹力等于电场力,从而确定电场强度的大小与方向;
(2)根据密度相同,可确定质量与半径立方关系;根据题意,可知电量与半径平方关系.从而由动能定理可算出粒子通过O2时的速率;
(3)由半径的不同,导致速度大小不一,从而出现洛伦兹力与电场力不等现象,根据其力大小确定向哪个极板偏转.
解答:解 (1)设半径为r的粒子加速后的速度为v,则

解得:
设区域II内电场强度为E,则
洛伦兹力等于电场力,即v qB=qE
解得:
电场强度方向竖直向上.
(2)设半径为r的粒子的质量为m、带电量为q、被加速后的速度为v,
则
而
由
解得:
(3)半径为r的粒子,在刚进入区域II时受到合力
为F合=qE-qvB=qB(v-v)
由 可知,
可知,
当r>r时,v<v,F合>0,粒子会向上极板偏转;
当r<r时,v>v,F合<0,粒子会向下极板偏转.
答:(1)图中区域II的电场强度 ;
;
(2)半径为r的粒子通过O2时的速率 ;
;
(3)由 可知,
可知,
当r>r时,v<v,F合>0,粒子会向上极板偏转;
当r<r时,v>v,F合<0,粒子会向下极板偏转.
点评:本题考查运用动能定理求带电粒子在电场中加速后的速度大小,再洛伦兹力与电场力关系来确定偏向何处.同时注意紧扣题意密度相同及电量与表面积成正比等隐含条件.
(2)根据密度相同,可确定质量与半径立方关系;根据题意,可知电量与半径平方关系.从而由动能定理可算出粒子通过O2时的速率;
(3)由半径的不同,导致速度大小不一,从而出现洛伦兹力与电场力不等现象,根据其力大小确定向哪个极板偏转.
解答:解 (1)设半径为r的粒子加速后的速度为v,则

解得:

设区域II内电场强度为E,则
洛伦兹力等于电场力,即v qB=qE
解得:

电场强度方向竖直向上.
(2)设半径为r的粒子的质量为m、带电量为q、被加速后的速度为v,
则

而

由

解得:

(3)半径为r的粒子,在刚进入区域II时受到合力
为F合=qE-qvB=qB(v-v)
由
 可知,
可知,当r>r时,v<v,F合>0,粒子会向上极板偏转;
当r<r时,v>v,F合<0,粒子会向下极板偏转.
答:(1)图中区域II的电场强度
 ;
;(2)半径为r的粒子通过O2时的速率
 ;
;(3)由
 可知,
可知,当r>r时,v<v,F合>0,粒子会向上极板偏转;
当r<r时,v>v,F合<0,粒子会向下极板偏转.
点评:本题考查运用动能定理求带电粒子在电场中加速后的速度大小,再洛伦兹力与电场力关系来确定偏向何处.同时注意紧扣题意密度相同及电量与表面积成正比等隐含条件.

练习册系列答案
相关题目
 (2011?甘肃二模)某研究性学习小组用如图(a)所示装置验证机械能守恒定律.让一个摆球由静止开始从A位置摆到B位置,若不考虑空气阻力,小球的机械能应该守恒,即
(2011?甘肃二模)某研究性学习小组用如图(a)所示装置验证机械能守恒定律.让一个摆球由静止开始从A位置摆到B位置,若不考虑空气阻力,小球的机械能应该守恒,即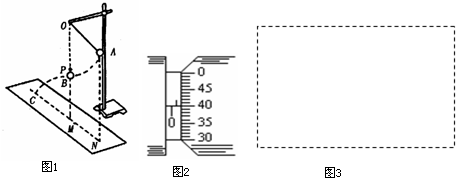

 某研究性学习小组用如图(a)所示装置验证机械能守恒定律.让一个摆球由静止开始从A位置摆到B位置,若不考虑空气阻力,小球的机械能应该守恒,即
某研究性学习小组用如图(a)所示装置验证机械能守恒定律.让一个摆球由静止开始从A位置摆到B位置,若不考虑空气阻力,小球的机械能应该守恒,即 某研究性学习小组用如图所示的装置探究牛顿第二定律.该小组在实验中确定的研究对象是小车,而且认为细线对小车的拉力等于砂桶和砂的总重力,也是小车所受的合外力.则对该实验,以下说法中不正确的是.
某研究性学习小组用如图所示的装置探究牛顿第二定律.该小组在实验中确定的研究对象是小车,而且认为细线对小车的拉力等于砂桶和砂的总重力,也是小车所受的合外力.则对该实验,以下说法中不正确的是.