题目内容
（2005?淮安模拟）天文工作者观测某行星的半径为R1，自转周期为T1，它有一颗卫星，轨道半径为R2，绕行星公转周期为T2，求：
（1）该行星的平均密度；
（2）该行星的同步卫星的速度．
（1）该行星的平均密度；
（2）该行星的同步卫星的速度．
分析：1、根据万有引力提供卫星圆周运动的向心力可以列式求出行星的质量M，进一步求密度；
2、该行星的同步卫星的周期与该行星的自转周期相同，根据万有引力提供向心力G
=m(
)2r，速度与周期的关系为v=
，以及第一问中求出行星质量M，化简可得速度v．
2、该行星的同步卫星的周期与该行星的自转周期相同，根据万有引力提供向心力G
| Mm |
| r2 |
| 2π |
| T1 |
| 2πr |
| T1 |
解答：解：（1）根据万有引力提供向心力：G
=m
-----①
得：M=
--------------------------②
根据密度的定义得：ρ=
=
=
------------③
（2）设同步卫星轨道半径为r，则：G
=m(
)2r---------④
速度与周期的关系为v=
---------------------⑤
由②④⑤式解得：v=
---------------------⑥
答：（1）该行星的平均密度为
；
（2）该行星的同步卫星的速度为
．
| Mm | ||
|
| 4π2R2 | ||
|
得：M=
4π2
| ||
G
|
根据密度的定义得：ρ=
| M |
| V |
| M | ||||
|
3π
| ||||
G
|
（2）设同步卫星轨道半径为r，则：G
| Mm |
| r2 |
| 2π |
| T1 |
速度与周期的关系为v=
| 2πr |
| T1 |
由②④⑤式解得：v=
| 2πR2 | |||||
|
答：（1）该行星的平均密度为
3π
| ||||
G
|
（2）该行星的同步卫星的速度为
| 2πR2 | |||||
|
点评：解决问题的关键是万有引力提供圆周运动的向心力，另要知道该行星的同步卫星的周期与该行星的自转周期相同这一点是解决本题第二问的关键．
练习册系列答案
相关题目
（2005?淮安模拟）如图所示，弹簧下面挂一质量为m的物体，物体在竖直方向上作振幅为A的简谐运动，当物体振动到最高点时，弹簧正好为原长．则物体在振动过程中（ ）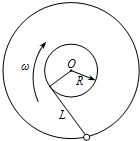
（2005?淮安模拟）如图所示，一条不可伸长的轻绳长为L，一端用手握住，另一端系一质量为m的小球．今使手握的一端在水平桌面上做半径为R，角速度为ω的匀速圆周运动，且使绳始终与半径为R的圆相切，小球也将在同一水平面内做匀速圆周运动，若人手做功的功率为P，求：