题目内容
如图所示，用一根长为l＝1m的细线，一端系一质量为m＝1kg的小球(可视为质点)，另一端固定在一光滑锥体顶端，锥面与竖直方向的夹角θ＝370，当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时，细线的张力为T．求(取g＝10m/s2，结果可用根式表示)：
1.若要小球离开锥面，则小球的角速度ω0至少为多大？
2.若细线与竖直方向的夹角为600，则小球的角速度ω＇为多大？
3.细线的张力T与小球匀速转动的加速度ω有关，请在坐标纸上画出ω的取值
范围在0到ω＇之间时的T—ω2的图象(要求标明关键点的坐标值)．
【答案】
1.
2.
3.
【解析】
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
（2008?江苏模拟）如图所示，用一根长为L的细绳一端固定在O点，另一端悬挂质量为m的小球A，为使细绳与竖直方向夹30°角且绷紧，小球A处于静止，则需对小球施加的最小力等于（ ）
如图所示，用一根长为L质量不计的细杆与一个上弧长为l0、下弧长为d0的金属线框的中点连接并悬挂于O点，悬点正下方存在一个上弧长为2l0、下弧长为2d0的方向垂直纸面向里的匀强磁场，且d0《L．先将线框拉开到如图所示位置，松手后让线框进入磁场，忽略空气阻力和摩擦．下列说法正确的是（ ）
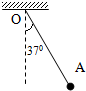如图所示，用一根长为L的细绳一端固定在O点，另一端悬挂质量为m的小球A，为使细绳与竖直方向夹370角且小球A保持静止状态，则需对小球施加第三个力，下列说法（ ）A、等于
| ||
B、等于
| ||
| C、等于mg时，一定竖直向上 | ||
| D、以上说法均不正确 |
如图所示，用一根长为L质量不计的细杆与一个上弧长为l0、下弧长为d0的金属线框的中点联结并悬挂于O点，悬点正下方存在一个上弧长为2l0、下弧长为2d0的方向垂直纸面向里的匀强磁场，且d0＜＜L，先将线框拉开到如图所示位置，松手后让线框进入磁场，忽略空气阻力和摩擦．下列说法正确的是（ ）| A、金属线框进入磁场时感应电流的方向为a→d→c→b→a | B、金属线框离开磁场时感应电流的方向为a→d→c→b→a | C、金属线框dc边进入磁场与ab边离开磁场的速度大小总是相等 | D、金属线框最终将停在最低点 |
