题目内容
(2007?淄博模拟)甲、乙两汽车均以20m/s的速度在公路上沿同方向正常行驶,乙车因遇到突发事件需紧急停车,其停车时的加速度为10m/s2,停下1分钟后,又以5m/s2的加速度启动到正常行驶速度,则乙车因停车而延误的时间和因停车而落后甲车的距离是( )
分析:求出列车减速到零再加速到原来速度这段时间内的位移,求出在这段位移内若以20m/s速度运行所需的时间,再求出实际通过这段位移的时间,两时间之差为停车所耽误的时间.
解答:解:乙车匀减速直线运动的位移x1=
=
m=20m,匀减速直线运动的时间t1=
=2s.
匀加速直线运动的位移x2=
=
m=40m,匀加速直线运动的时间t0=
=
s=4s.
运动的总位移x=x1+x2=60m.
若不停车所需的时间t=
=3s.因临时停车而延误的时间为
△t=t1+t2+t′-t=2+4+60-3=63s.
在此时间内甲车运动的位移为x′=v△t=20×63m=1260m,
故因停车而落后甲车的距离是1260m.
故选B
| v2 |
| 2a1 |
| 202 |
| 2×10 |
| v |
| a1 |
匀加速直线运动的位移x2=
| v2 |
| 2a2 |
| 202 |
| 2×5 |
| v |
| a2 |
| 20 |
| 5 |
运动的总位移x=x1+x2=60m.
若不停车所需的时间t=
| x |
| v |
△t=t1+t2+t′-t=2+4+60-3=63s.
在此时间内甲车运动的位移为x′=v△t=20×63m=1260m,
故因停车而落后甲车的距离是1260m.
故选B
点评:解决本题的关键掌握匀变速直线运动的速度位移公式v2-v02=2ax以及速度时间公式v=v0+at灵活应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2007?淄博模拟)如图所示,甲是一个带正电的小物块,乙是一个不带电的绝缘物块,甲、乙叠放在一起静置于粗糙的水平地板上,地板上方空间有水平方向的匀强磁场.现用水平恒力拉乙物块,使甲、乙无相对滑动地一起水平向左加速运动,在加速运动阶段( )
(2007?淄博模拟)如图所示,甲是一个带正电的小物块,乙是一个不带电的绝缘物块,甲、乙叠放在一起静置于粗糙的水平地板上,地板上方空间有水平方向的匀强磁场.现用水平恒力拉乙物块,使甲、乙无相对滑动地一起水平向左加速运动,在加速运动阶段( ) (2007?淄博模拟)如图,长为L的轻杆一端固定一质量为m的小球,另一端有固定轴O,杆可在竖直平面内绕轴O无摩擦转动.已知小球通过最低点Q时,速度的大小为
(2007?淄博模拟)如图,长为L的轻杆一端固定一质量为m的小球,另一端有固定轴O,杆可在竖直平面内绕轴O无摩擦转动.已知小球通过最低点Q时,速度的大小为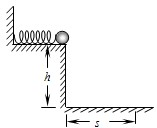 (2007?淄博模拟)一同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关系,他的实验如下:在离地面高度为h的光滑水平桌面上,沿着与桌子边缘垂直的方向放置一轻质弹簧.其左端固定,右端与质量为m的一个钢球接触,当弹簧处于自然长度时,小钢球恰好在桌子边缘,如图所示.让钢球向左压缩弹簧一段距离后由静止释放,使钢球沿水平方向射出桌面,小球在空中飞行后落到水平地面,水平距离为s.
(2007?淄博模拟)一同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关系,他的实验如下:在离地面高度为h的光滑水平桌面上,沿着与桌子边缘垂直的方向放置一轻质弹簧.其左端固定,右端与质量为m的一个钢球接触,当弹簧处于自然长度时,小钢球恰好在桌子边缘,如图所示.让钢球向左压缩弹簧一段距离后由静止释放,使钢球沿水平方向射出桌面,小球在空中飞行后落到水平地面,水平距离为s.