��Ŀ����
 ��ͼ��ʾ����ֱ������ϵ xoy �ĵ�һ�����ڴ����� y �Ḻ����ǿΪ E ����ǿ�糡���ڵ��������ڴ��ڴ�ֱֽ�����⡢�Ÿ�Ӧǿ��Ϊ B ����ǿ�ų����ڴų���糡�ֽ��ߵ� x ������һ����ı�����㣮һ����Ϊ m������Ϊ+q�����ٶ�Ϊ��Ĵ������ӣ�������Ϊ�� x 0��y 0���� P �㿪ʼ���糡���٣�������㴹ֱ����ų�������ÿ�δ�Խ������ʱ�伫�̣����˶����䣬�䴩Խ����ٶ���ÿ�δ�Խǰ�ٶȵ� k ���� k��1�������ƴ�������������������
��ͼ��ʾ����ֱ������ϵ xoy �ĵ�һ�����ڴ����� y �Ḻ����ǿΪ E ����ǿ�糡���ڵ��������ڴ��ڴ�ֱֽ�����⡢�Ÿ�Ӧǿ��Ϊ B ����ǿ�ų����ڴų���糡�ֽ��ߵ� x ������һ����ı�����㣮һ����Ϊ m������Ϊ+q�����ٶ�Ϊ��Ĵ������ӣ�������Ϊ�� x 0��y 0���� P �㿪ʼ���糡���٣�������㴹ֱ����ų�������ÿ�δ�Խ������ʱ�伫�̣����˶����䣬�䴩Խ����ٶ���ÿ�δ�Խǰ�ٶȵ� k ���� k��1�������ƴ���������������������1���������ӵ�һ�δ�Խ��������ų���Բ���˶��İ뾶 R 1��
��2���������ӵڶ��δ�Խ��������糡�ﵽ��ߵ�������� y1��
��3���ӿ�ʼ�������δ�Խ��������õ���ʱ�� t��
��4�����������ӵ��Ĵδ�Խ�����ʱ�պõ�������ԭ�� O���� P ������� x0�������� y0Ӧ����Ĺ�ϵ��
��������1�����ݶ��ܶ���������ӵ�һ�ε�������ʱ���ٶȣ��Ӷ��ó���һ�δ�Խ�������ٶȣ��������������ṩ����������������ӵ�һ�δ�Խ��������ų���Բ���˶��İ뾶��
��2����Խ����ٶ���ÿ�δ�Խǰ�ٶȵ� k ������֪�ڶ��δ�Խ�������ٶȣ����ݶ��ܶ�������������ӵڶ��δ�Խ��������糡�ﵽ��ߵ�������꣮
��3���ӿ�ʼ�������δ�Խ���������У��ڴų����˶����Բ�ܣ��������ڹ�ʽ����ڴų����˶���ʱ�䣬�ڵ糡�����ȱ���ֱ���˶�������λ��ʱ�乫ʽ����ڵ糡���˶���ʱ�䣬�Ӷ������ʱ�䣮
��4���ֱ������һ�δ�Խ�����͵����δ����������ڴų����˶��Ĺ���뾶��ץסx0=2R1+2R2��� P ������� x0�������� y0Ӧ����Ĺ�ϵ��
��2����Խ����ٶ���ÿ�δ�Խǰ�ٶȵ� k ������֪�ڶ��δ�Խ�������ٶȣ����ݶ��ܶ�������������ӵڶ��δ�Խ��������糡�ﵽ��ߵ�������꣮
��3���ӿ�ʼ�������δ�Խ���������У��ڴų����˶����Բ�ܣ��������ڹ�ʽ����ڴų����˶���ʱ�䣬�ڵ糡�����ȱ���ֱ���˶�������λ��ʱ�乫ʽ����ڵ糡���˶���ʱ�䣬�Ӷ������ʱ�䣮
��4���ֱ������һ�δ�Խ�����͵����δ����������ڴų����˶��Ĺ���뾶��ץסx0=2R1+2R2��� P ������� x0�������� y0Ӧ����Ĺ�ϵ��
����⣺��1����һ�ε�������ʱ�ٶ�Ϊv0
qEyo=
mvo2��v0=
��һ�δ�Խ�������ٶ�Ϊv1=k
��qv1B=m
���õ�һ���ڴų�����Բ���˶��뾶Ϊ R1=
=
��2���ڶ��δ�Խ�������ٶ�Ϊv2=k2
-qEy1=0-
mv22����y1=k4y0
��3����yo=
t02���õ�һ�ε��������ʱ��Ϊ t0=
Բ���˶�������T=
��һ���ڴų�����Բ���˶�ʱ��Ϊ t1=
=
�ڶ��δ�Խ��������ߵ�ʱ��Ϊ t2=
=k 2
�ӿ�ʼ�������δ�Խ�����������ʱ��
t=t0+t1+2t2=��1+2 k2��
+
��4�������δ�Խ��������ٶ�Ϊv 3=k 3
�ڶ����ڴų�����Բ���˶��뾶ΪR2=
x0=2R1+2R2=�� 2 k+2 k 3��
�𣺣�1���������ӵ�һ�δ�Խ��������ų���Բ���˶��İ뾶Ϊ
��
��2���������ӵڶ��δ�Խ��������糡�ﵽ��ߵ��������y1=k4y0
��3���ӿ�ʼ�������δ�Խ��������õ���ʱ��Ϊ��1+2 k2��
+
��
��4��P ������� x0�������� y0Ӧ����Ĺ�ϵΪ��x0=�� 2 k+2 k 3��
��
qEyo=
| 1 |
| 2 |
|
��һ�δ�Խ�������ٶ�Ϊv1=k
|
��qv1B=m
| v12 |
| R1 |
| mv1 |
| qB |
|
��2���ڶ��δ�Խ�������ٶ�Ϊv2=k2
|
-qEy1=0-
| 1 |
| 2 |
��3����yo=
| 1 |
| 2 |
| qE |
| m |
|
Բ���˶�������T=
| 2��m |
| qB |
��һ���ڴų�����Բ���˶�ʱ��Ϊ t1=
| T |
| 2 |
| ��m |
| qB |
�ڶ��δ�Խ��������ߵ�ʱ��Ϊ t2=
| v2 |
| a |
|
�ӿ�ʼ�������δ�Խ�����������ʱ��
t=t0+t1+2t2=��1+2 k2��
|
| ��m |
| qB |
��4�������δ�Խ��������ٶ�Ϊv 3=k 3
|
�ڶ����ڴų�����Բ���˶��뾶ΪR2=
|
x0=2R1+2R2=�� 2 k+2 k 3��
|
�𣺣�1���������ӵ�һ�δ�Խ��������ų���Բ���˶��İ뾶Ϊ
|
��2���������ӵڶ��δ�Խ��������糡�ﵽ��ߵ��������y1=k4y0
��3���ӿ�ʼ�������δ�Խ��������õ���ʱ��Ϊ��1+2 k2��
|
| ��m |
| qB |
��4��P ������� x0�������� y0Ӧ����Ĺ�ϵΪ��x0=�� 2 k+2 k 3��
|
���������⿼����������ڵ糡�ʹų��е��˶����ؼ�֪�������ڴų���������Բ���˶����ڵ糡�����ȱ���ֱ���˶�������ţ�ٵڶ����ɽ���˶�ѧ��ʽ������⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
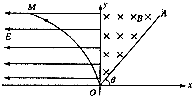 ��ͼ��ʾ����ֱ������ƽ��ĵ�I��������һ��ǿ�ų����Ÿ�Ӧǿ��ΪB��ֱ��OA�Ǵų��Ҳ�ı߽磮�ڵڢ����������ڵ糡ǿ�ȴ�СΪE��ˮƽ�������ǿ�糡��y���ǵ糡���ų�����ķֽ������ߣ�OM���㷽��x=-ky2��k��0������һ�������Ϊq������Ϊm�ĸ����ӣ��������ƣ�������OM��ijһ���ɾ�ֹ�ͷţ���Խy�����ų��У�
��ͼ��ʾ����ֱ������ƽ��ĵ�I��������һ��ǿ�ų����Ÿ�Ӧǿ��ΪB��ֱ��OA�Ǵų��Ҳ�ı߽磮�ڵڢ����������ڵ糡ǿ�ȴ�СΪE��ˮƽ�������ǿ�糡��y���ǵ糡���ų�����ķֽ������ߣ�OM���㷽��x=-ky2��k��0������һ�������Ϊq������Ϊm�ĸ����ӣ��������ƣ�������OM��ijһ���ɾ�ֹ�ͷţ���Խy�����ų��У� ��2013?������ģ����ͼ��ʾ����ֱ������xOyƽ��y����ࣨ��y�ᣩ��һ��y�Ḻ�����ǿ�糡��һ����Ϊm������Ϊq�Ĵ��������Ӵ�x����P�����ٶȦ�0��x���������糡����y����Q���뿪�糡ʱ�ٶȱ�Ϊ2��0��Q������Ϊ��0��-d������y���Ҳ���һ������ƽ�洹ֱ�ľ�����ǿ�ų�����ͼ��δ���������ӹ�Q������˶�һ�ξ����Ž���ų������ų��Ÿ�Ӧǿ�ȴ�С
��2013?������ģ����ͼ��ʾ����ֱ������xOyƽ��y����ࣨ��y�ᣩ��һ��y�Ḻ�����ǿ�糡��һ����Ϊm������Ϊq�Ĵ��������Ӵ�x����P�����ٶȦ�0��x���������糡����y����Q���뿪�糡ʱ�ٶȱ�Ϊ2��0��Q������Ϊ��0��-d������y���Ҳ���һ������ƽ�洹ֱ�ľ�����ǿ�ų�����ͼ��δ���������ӹ�Q������˶�һ�ξ����Ž���ų������ų��Ÿ�Ӧǿ�ȴ�С ��ͼ��ʾ����ֱ������xOyƽ��y����ࣨ��y�ᣩ��һ��y�Ḻ�����ǿ�糡��һ����Ϊm������Ϊq�Ĵ��������Ӵ�x����P�����ٶ�v0��x���������糡����y����Q���뿪�糡ʱ�ٶȷ�����y�Ḻ��нǦ�=30�㣬Q������Ϊ��0��-d������y���Ҳ���һ������ƽ�洹ֱ���н���ǿ�ų�����ͼ��δ���������ų��Ÿ�Ӧǿ�ȴ�СB=
��ͼ��ʾ����ֱ������xOyƽ��y����ࣨ��y�ᣩ��һ��y�Ḻ�����ǿ�糡��һ����Ϊm������Ϊq�Ĵ��������Ӵ�x����P�����ٶ�v0��x���������糡����y����Q���뿪�糡ʱ�ٶȷ�����y�Ḻ��нǦ�=30�㣬Q������Ϊ��0��-d������y���Ҳ���һ������ƽ�洹ֱ���н���ǿ�ų�����ͼ��δ���������ų��Ÿ�Ӧǿ�ȴ�СB= ��ͼ��ʾ����ֱ������xoy�ĵ�һ�����зֲ���ָ��y�᷽�����ǿ�糡���ڵ��������зֲ��Ŵ�ֱֽ�����﷽�����ǿ�ų���һ������Ϊm�����磫q������(��������)��A��(0��3)�Գ���V0��120m/sƽ��x������糡����Ȼ��ӵ糡�������ų����ִӴų�����糡������ֻͨ��x���ϵ�P��(6��0)��Q��(8��0)��һ�Σ���֪�����ӵĺ��ʱ�Ϊq/m��108c/kg��
��ͼ��ʾ����ֱ������xoy�ĵ�һ�����зֲ���ָ��y�᷽�����ǿ�糡���ڵ��������зֲ��Ŵ�ֱֽ�����﷽�����ǿ�ų���һ������Ϊm�����磫q������(��������)��A��(0��3)�Գ���V0��120m/sƽ��x������糡����Ȼ��ӵ糡�������ų����ִӴų�����糡������ֻͨ��x���ϵ�P��(6��0)��Q��(8��0)��һ�Σ���֪�����ӵĺ��ʱ�Ϊq/m��108c/kg�� ��x���������糡����y����Q���뿪�糡ʱ�ٶȷ�����y�Ḻ��н�
��x���������糡����y����Q���뿪�糡ʱ�ٶȷ�����y�Ḻ��н� ��Q������Ϊ��0��-d������y���Ҳ���һ������ƽ�洹ֱ���н���ǿ�ų�����ͼ��δ���������ų��Ÿ�Ӧǿ�ȴ�С
��Q������Ϊ��0��-d������y���Ҳ���һ������ƽ�洹ֱ���н���ǿ�ų�����ͼ��δ���������ų��Ÿ�Ӧǿ�ȴ�С �������ܴ�����ԭ��O��x�Ḻ���ٽ���糡������������������
�������ܴ�����ԭ��O��x�Ḻ���ٽ���糡������������������