题目内容
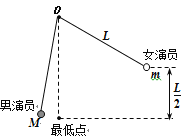
【题目】如图所示，倾角为
的斜面OB段粗糙（足够长），其余部分光滑，在斜面O点上方静止一质量均匀分布长度为L的薄板，薄板下端与O点之间的距离为2L，薄板与OB段的动摩擦因数μ=2tanθ。现由静止释放薄板，薄板沿斜面向下运动，已知当薄板部分通过O点时，薄板所受摩擦力大小是薄板在斜面OB段上重量的μcosθ倍。以O点为坐标原点，沿斜面向下建立直线坐标轴Ox。从薄板下端刚到达O点开始，薄板所受的摩擦力Ff、速度v、加速度a，动能Ek与薄板下端相对O点的位移x的关系图象为
A. 
B. 
C. 
D. 
【答案】ACD
【解析】当薄板的下端经过O点的距离为x时，所受的摩擦力为
，全部进入OB段后摩擦力为 
，则选项A正确；当薄板的下端经过O点的距离为x时薄板的加速度
，则加速度随x的增加而减小，然后反向增加，当全部进入OB区域时x=2L，此时a=-gsinθ则选项B错误，C正确；当薄板的下端经过O点的距离为x时，由动能定理：
；全部进入OB区域后动能：
， 选择D正确；故选ACD.
练习册系列答案
53随堂测系列答案
相关题目
