题目内容
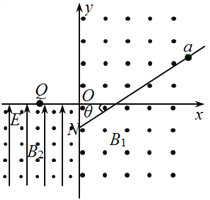
【题目】如图所示，Oxy为直角坐标系，在-d≤x≤o范圈内有沿+y方向的匀强电场，场强大小为E;在x≤-d和x≥0范圈内有方向均垂直于Oxy平面向里的匀强磁场，磁感应强度大小均为B。一带正电的粒子从（－d,0)处沿x轴正方向以速度V0射入电场，从y轴上的P1(0, )点第一次离开电场，从y轴上的M1(0,d)点第二次进入电场。不计粒子的重力。求
(1)电场强度E和磁感应强度B的比值;
(2)粒子第3次在右侧磁场（x≥0)运动的过程中，到y轴的最远距离。
【答案】
【解析】（1）粒子第1次在电场中运动，加速度大小
通过电场的时间
沿+y方向的位移
联立解得
粒子第1次进入右侧的磁场时，设速度v的偏向角为
，速度
在右侧磁场中，粒子第1次做圆周运动的半径
在右侧磁场中，粒子第1次运动的入射点和出射点间的距离
由题意
联立解得
，故
（2）粒子在电场中运动时，因电场力沿+y方向，故粒子速度的水平分量恒为
，根据
可知，粒子每次在电场中运动的时间均相同，而粒子每次在电场运动的加速度不变，根据对称性，可将粒子在电场中的运动累积起来，等效为粒子在电场中以水平初速度
做类平抛运动。
粒子第n此通过y轴进入右侧磁场时，设沿+y方向的速度分量为
，速度方向与x轴的即将为
，则
，n=1,2,3……
，由②③解得
由以上三式解得
由（1）中的
、
、
解得
由
可知，粒子每次进出磁场的
均相同，则
粒子第n次在右侧磁场中运动，到y轴最远的距离
联立解得
当n=3时， 
练习册系列答案
相关题目
