题目内容
 (2011?海淀区一模)如图所示,一个物块A(可看成质点)放在足够长的平板小车B的右端,A、B一起以v0的水平初速度沿光滑水平面向左滑行.左边有一固定的竖直墙壁,小车B与墙壁相碰,碰撞时间极短,且碰撞前、后无动能损失.已知物块A与小车B的水平上表面间的动摩擦因数为μ,重力加速度为g.
(2011?海淀区一模)如图所示,一个物块A(可看成质点)放在足够长的平板小车B的右端,A、B一起以v0的水平初速度沿光滑水平面向左滑行.左边有一固定的竖直墙壁,小车B与墙壁相碰,碰撞时间极短,且碰撞前、后无动能损失.已知物块A与小车B的水平上表面间的动摩擦因数为μ,重力加速度为g.(1)若A、B的质量均为m,求小车与墙壁碰撞后的运动过程中,物块A所受摩擦力的冲量大小和方向;
(2)若A、B的质量比为k,且k<1,求物块A在小车B上发生相对运动的过程中物块A对地的位移大小;
(3)若A、B的质量比为k,且k=2,求小车第一次与墙壁碰撞后的运动过程所经历的总时间.
分析:(1)碰后动量守恒,根据动量守恒和动量定理列方程可求得结果.
(2)碰后A、B作用过程中系统动量守恒,最终AB速度相同,根据动量守恒和能量守恒列方程可正确解答.
(3)分析清楚运动状态,由于摩擦的存在,经B与墙壁多次碰撞后最终A、B一起停在墙角,每次碰后系统动量守恒,根据动量守恒、功能关系列方程求出每次碰撞后运动时间,然后找出规律,利用数学知识求解即可.
(2)碰后A、B作用过程中系统动量守恒,最终AB速度相同,根据动量守恒和能量守恒列方程可正确解答.
(3)分析清楚运动状态,由于摩擦的存在,经B与墙壁多次碰撞后最终A、B一起停在墙角,每次碰后系统动量守恒,根据动量守恒、功能关系列方程求出每次碰撞后运动时间,然后找出规律,利用数学知识求解即可.
解答:解:(1)设小车B与墙碰撞后物块A与小车B所达到的共同速度大小为v,设向右为正方向,则由动量守恒定律得:
mv0-mv0=2mv
解得:v=0.
对物块A,由动量定理得摩擦力对物块A的冲量:I=0-(-mv0)=mv0,冲量方向水平向右.
故物块A所受摩擦力的冲量大小为I=mv0,方向水平向右.
(2)设A和B的质量分别为km和m,小车B与墙碰撞后物块A与小车B所达到的共同速度大小为v′,木块A的位移大小为s.设向右为正方向,则由动量守恒定律得:则
mv0-kmv0=(m+km)v′
解得:v′=
v0
对木块A由动能定理得:
-μkmgs=
kmv′2-
km
代入数据解得:s=
.
故物块A在小车B上发生相对运动的过程中物块A对地的位移大小为:s=
.
(3)当k=2时,根据题意由于摩擦的存在,经B与墙壁多次碰撞后最终A、B一起停在墙角.A与B发生相对运动的时间t0可等效为A一直做匀减速运动到速度等于0的时间,在A与B发生相对滑动的整个过程,对A应用动量定理:-2mgμt0=0-2mv0
解得时间:t0=
,
设第1次碰后A、B达到的共同速度为v1,B碰墙后,A、B组成的系统,没有外力作用,水平方向动量守恒,设水平向右为正方向,由动量守恒定律,得:
mv0-2mv0=(2m+m)v1
即:v1=-
v0(负号表示v1的方向向左)
第1次碰后小车B向左匀速运动的位移等于向右匀减速运动到速度大小为v1这段运动的位移s1
对小车B,由动能定理得-μ2mgs1=
mv12-
mv02
解得:s1=
第1次碰后小车B向左匀速运动时间:t1=
=
设第2次碰后共速为v2,由动量守恒定律,得:mv1-2mv1=(2m+m)v2
即:v2=
v1=-
v0
第2次碰后小车B向左匀速运动的位移等于向右匀减速运动到速度大小为v2这段运动的位移s2,对小车B,由动能定理得:
-μ2mgs2=
m v22-
mv12
解得:s2=
?
第2次碰后小车B向左匀速运动时间:t2=
=
同理,设第3次碰后共速为v3,碰后小车B向左匀速运动的位移为s3,则由动量守恒定律,得:v3=
v2=-
v0
s3=
?
第3次碰后小车B向左匀速运动时间:t3=
=
由此类推,第n次碰墙后小车B向左匀速运动时间:tn=
.
第1次碰墙后小车B向左匀速运动时间即B从第一次撞墙后每次向左匀速运动时间为首项为t1,末项为tn,公比为
的无穷等比数列.即B从第一次与墙壁碰撞后匀速运动的总时间t匀=t1+t2+t3+…+tn=
故从第一次B与墙壁碰撞后运动的总时间:t总=t0+t匀=
.
mv0-mv0=2mv
解得:v=0.
对物块A,由动量定理得摩擦力对物块A的冲量:I=0-(-mv0)=mv0,冲量方向水平向右.
故物块A所受摩擦力的冲量大小为I=mv0,方向水平向右.
(2)设A和B的质量分别为km和m,小车B与墙碰撞后物块A与小车B所达到的共同速度大小为v′,木块A的位移大小为s.设向右为正方向,则由动量守恒定律得:则
mv0-kmv0=(m+km)v′
解得:v′=
| 1-k |
| 1+k |
对木块A由动能定理得:
-μkmgs=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
代入数据解得:s=
2k
| ||
| μg(1+k)2 |
故物块A在小车B上发生相对运动的过程中物块A对地的位移大小为:s=
2k
| ||
| μg(1+k)2 |
(3)当k=2时,根据题意由于摩擦的存在,经B与墙壁多次碰撞后最终A、B一起停在墙角.A与B发生相对运动的时间t0可等效为A一直做匀减速运动到速度等于0的时间,在A与B发生相对滑动的整个过程,对A应用动量定理:-2mgμt0=0-2mv0
解得时间:t0=
| v0 |
| μg |
设第1次碰后A、B达到的共同速度为v1,B碰墙后,A、B组成的系统,没有外力作用,水平方向动量守恒,设水平向右为正方向,由动量守恒定律,得:
mv0-2mv0=(2m+m)v1
即:v1=-
| 1 |
| 3 |
第1次碰后小车B向左匀速运动的位移等于向右匀减速运动到速度大小为v1这段运动的位移s1
对小车B,由动能定理得-μ2mgs1=
| 1 |
| 2 |
| 1 |
| 2 |
解得:s1=
2
| ||
| 9μg |
第1次碰后小车B向左匀速运动时间:t1=
| s1 |
| v1 |
| 2v0 |
| 3μg |
设第2次碰后共速为v2,由动量守恒定律,得:mv1-2mv1=(2m+m)v2
即:v2=
| 1 |
| 3 |
| 1 |
| 32 |
第2次碰后小车B向左匀速运动的位移等于向右匀减速运动到速度大小为v2这段运动的位移s2,对小车B,由动能定理得:
-μ2mgs2=
| 1 |
| 2 |
| 1 |
| 2 |
解得:s2=
| 1 |
| 92 |
2
| ||
| μg |
第2次碰后小车B向左匀速运动时间:t2=
| s2 |
| v2 |
| 2v0 |
| 32μg |
同理,设第3次碰后共速为v3,碰后小车B向左匀速运动的位移为s3,则由动量守恒定律,得:v3=
| 1 |
| 3 |
| 1 |
| 33 |
s3=
| 1 |
| 93 |
2
| ||
| μg |
第3次碰后小车B向左匀速运动时间:t3=
| s3 |
| v3 |
| 2v0 |
| 33μg |
由此类推,第n次碰墙后小车B向左匀速运动时间:tn=
| 2v0 |
| 3nμg |
第1次碰墙后小车B向左匀速运动时间即B从第一次撞墙后每次向左匀速运动时间为首项为t1,末项为tn,公比为
| 1 |
| 3 |
| v0 |
| μg |
故从第一次B与墙壁碰撞后运动的总时间:t总=t0+t匀=
| 2v0 |
| μg |
点评:本题全面考查了动量守恒和功能关系的应用,尤其是第(3)问,要通过关系式找出规律,考查了学生应用数学知识解决物理问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2011?海淀区一模)如图所示是研究平行板电容器的电容大小与哪些因素有关的实验装置.将充好电的平行板电容器与电源断开并一板接地,另一板与外壳接地的静电计相连.当改变电容器两板之间的距离和两板正对面积时,实验发现静电计指针的张角随之改变.若电容器的电容用C表示,两板之间距离用d表示,两板正对面积用S表示,静电计指针张角用θ表示.则以下对该实验现象的判断正确的是( )
(2011?海淀区一模)如图所示是研究平行板电容器的电容大小与哪些因素有关的实验装置.将充好电的平行板电容器与电源断开并一板接地,另一板与外壳接地的静电计相连.当改变电容器两板之间的距离和两板正对面积时,实验发现静电计指针的张角随之改变.若电容器的电容用C表示,两板之间距离用d表示,两板正对面积用S表示,静电计指针张角用θ表示.则以下对该实验现象的判断正确的是( )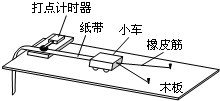 (2011?海淀区一模)(1)“探究动能定理”的实验装置如图所示,当小车在两条橡皮筋作用下弹出时,橡皮筋对小车做的功记为W0.当用4条、6条、8条…完全相同的橡皮筋并在一起进行第2次、第3次、第4次…实验时,橡皮筋对小车做的功记为2W0、3W0、4W0…,每次实验中由静止弹出的小车获得的最大速度可由打点计时器所打的纸带测出.关于该实验,下列说法正确的是
(2011?海淀区一模)(1)“探究动能定理”的实验装置如图所示,当小车在两条橡皮筋作用下弹出时,橡皮筋对小车做的功记为W0.当用4条、6条、8条…完全相同的橡皮筋并在一起进行第2次、第3次、第4次…实验时,橡皮筋对小车做的功记为2W0、3W0、4W0…,每次实验中由静止弹出的小车获得的最大速度可由打点计时器所打的纸带测出.关于该实验,下列说法正确的是