题目内容
 如图所示,Q为固定的正点电荷,A、B两点位于Q的正上方和Q相距分别为h和0.25h,将另一点电荷从A点由静止释放,运动到B点时速度刚好又变为零.若此电荷在A点处的加速度大小为3g/4,则此电荷在B点处的加速度a 为( )
如图所示,Q为固定的正点电荷,A、B两点位于Q的正上方和Q相距分别为h和0.25h,将另一点电荷从A点由静止释放,运动到B点时速度刚好又变为零.若此电荷在A点处的加速度大小为3g/4,则此电荷在B点处的加速度a 为( )分析:Q为固定的正点电荷,另一点电荷从 A点由静止释放,由于库仑斥力作用,运动到B点时速度正好又变为零.则由库仑定律与牛顿第二定律可求出电荷在A处的加速度,从而再次列出牛顿第二定律可求出电荷在B处的加速度.
解答:解:这一电荷必为正电荷,设其电荷量为q,由牛顿第二定律,
在A点时:mg-k
=m
g
在B点时:k
-mg=ma
解得:a=3g,方向竖直向上,故C正确
故选C
在A点时:mg-k
| h2 |
| 3 |
| 4 |
在B点时:k
| (0.25h)2 |
解得:a=3g,方向竖直向上,故C正确
故选C
点评:本题是库仑定律与牛顿第二定律,及动能定理,同时还涉及电场力做功的综合运用.另一点电荷在点电荷的电场中受到变化的库仑力,加速度大小是变化的.

练习册系列答案
相关题目
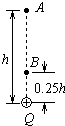 如图所示,Q为固定的正点电荷,A、B两点在Q的正上方和 Q相距分别为 h和0.25h,将另一点电荷从 A点由静止释放,运动到B点时速度正好又变为零.若此电荷在A点处的加速度大小为
如图所示,Q为固定的正点电荷,A、B两点在Q的正上方和 Q相距分别为 h和0.25h,将另一点电荷从 A点由静止释放,运动到B点时速度正好又变为零.若此电荷在A点处的加速度大小为 (2006?湖北模拟)如图所示,+Q为固定的正电荷,在它的电场中,一电荷量为+q的粒子,从o点以沿ob方向的初速度v0开始运动.若粒子只受电场力作用,则它的运动轨迹可能是图中的( )
(2006?湖北模拟)如图所示,+Q为固定的正电荷,在它的电场中,一电荷量为+q的粒子,从o点以沿ob方向的初速度v0开始运动.若粒子只受电场力作用,则它的运动轨迹可能是图中的( ) (2005?淮安二模)如图所示,+Q为固定的正电荷,在它的电场中,一电荷量为+q的粒子,从a点以沿ab方向的初速度v0开始运动.若粒子只受电场力作用,则它的运动轨迹不可能是图中的( )
(2005?淮安二模)如图所示,+Q为固定的正电荷,在它的电场中,一电荷量为+q的粒子,从a点以沿ab方向的初速度v0开始运动.若粒子只受电场力作用,则它的运动轨迹不可能是图中的( ) 如图所示,Q为固定的正点电荷(Q未知),A、B两点在Q的正上方和 Q相距分别为 h和0.25h,将另一电量为q,质量为m的正点电荷从 A点由静止释放,在A点处的加速度大小为
如图所示,Q为固定的正点电荷(Q未知),A、B两点在Q的正上方和 Q相距分别为 h和0.25h,将另一电量为q,质量为m的正点电荷从 A点由静止释放,在A点处的加速度大小为