题目内容
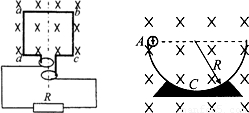
(18分)如图示,竖直平面内半圆形管道ADB固定在CD杆上,AB为直径,CD过圆心O且与AB垂直,半圆管道右半BD部分光滑,左半AD部分有摩擦,圆管道半径R=OB=0.2m,E点为圆管道BD中的一点,OE与CD夹角为θ=600 ,两个完全相同的可看作质点的小球,球直径略小于管道内径,小球质量m=0.1kg ,g=10m/s2 ,求:
(1)如图甲所示,当圆管道绕CD杆匀速转动时,要使小球稳定在管道中的E点,角速度ω应该多大?
(2)如图乙所示,圆管道保持静止,在圆管道D点处放置一静止小球,另一小球由静止开始从B端管口放入,该球经过D点时(未与另一小球相碰)对管道的压力?
(3)接(2)问,两球在D点相碰(碰撞时间极短)后粘在一起能运动到最高点F,OF与CD夹角为α=370 ,求此过程中摩擦力所做的功?

解:(1)小球在E点时受重力和管道的弹力,其合力提供向心力
由牛顿第二定律可得
![]() ………………….(2分)
………………….(2分)
![]() (1分)
(1分)
![]() ………………………..(1分)
………………………..(1分)
(2)设小球运动到D点时速度为v1 ,由机械能守恒定律可得
![]() ……….(2分)
……….(2分)
![]() …………….(1分)
…………….(1分)
设小球受到管道的弹力为N2,沿半径方向由牛顿第二定律可得
![]() ………………….(2分)
………………….(2分)
![]() ………………………………..(1分)
………………………………..(1分)
根据牛顿第三定律,小球过E点时对管道的压力F=1.5N (1分)
(3)设碰后瞬间两球的速度为v2,根据动量守恒定律
![]() ……………………………….(2分)
……………………………….(2分)
![]() (1分)
(1分)
设摩擦力做功为w,由动能定理可得
![]() …………(3分)
…………(3分)
![]() ……………………………………….(1分)
……………………………………….(1分)

练习册系列答案
相关题目
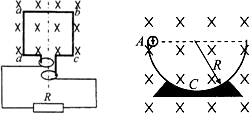 (1)如图所示,线圈abcd的面积是0.05m2,共100匝;线圈总电阻r=1Ω,外接电阻R=9Ω,匀强磁场的磁感应强度B=
(1)如图所示,线圈abcd的面积是0.05m2,共100匝;线圈总电阻r=1Ω,外接电阻R=9Ω,匀强磁场的磁感应强度B=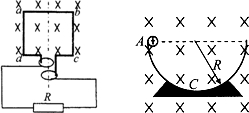
 T,线圈以角速度ω=100πrad/s匀速转动.
T,线圈以角速度ω=100πrad/s匀速转动.