Question

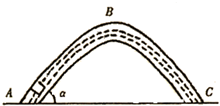
一封闭的弯曲的玻璃管处于竖直平面内，其中充满某种液体，内有一密度为液体密度一半的木块，从管的A端由静止开始运动，木块和管壁间动摩擦因数μ＝0.5，管两臂长AB＝BC＝L＝2 m，顶端B处为一小段光滑圆弧，两臂与水平面成α＝37°角，如图所示．求：

(1)木块从A到达B时的速率；

(2)木块从开始运动到最终静止经过的路程．

Answer 1

答案：
解析：

解：木块受四个力作用，如图所示 　　其中重力和浮力的合力竖直向上，大小为F＝F浮－mg，而F浮＝ρ液Vg＝2ρ木Vg＝2 mg，故F＝mg．在垂直于管壁方向有：FN＝Fcosα＝mgcosα，在平行管方向受滑动摩擦力Ff ＝μN＝μmgcos，比较可知，Fsinα＝mgsinα＝0.6 mg，Ff＝0.4mg，Fsinα＞Ff．故木块从A到B做匀加速运动，滑过B后F的分布和滑动摩擦力均为阻力，做匀减速运动，未到C之前速度即已为零，以后将在B两侧管间来回运动，但离B点距离越来越近，最终只能静止在B处． 　　(1)木块从A到B过程中，由动能定理有：FLsinα－FfL＝1/2 mυ 　　代入F、Ff各量得υB＝＝2＝2.83m/s． 　　(2)木块从开始运动到最终静止，运动的路程设为s，由动能定理有：FLsinα－FfS＝EK＝0 　　代入各量得s＝＝3 m